
| A. | ±3 | B. | ±2$\sqrt{2}$ | C. | ±2 | D. | ±$\sqrt{2}$ |
分析 设A,B到准线的距离分别为2a,a,由抛物线的定义可得|AB|=3a,利用锐角三角函数的定义即可得出直线AB的斜率.
解答 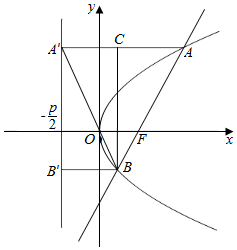 解:设A在第一象限,直线AB的倾斜角为α.
解:设A在第一象限,直线AB的倾斜角为α.
过B作准线的垂线BB′,作AA′的垂线BC,
∵|AB|=|A1B|,∴C是AA′的中点.
设|BB′|=a,则|AA′|=2a,∴|AB|=|AA′|+|BB′|=3a.
∴cosα=cos∠BAC=$\frac{AC}{AB}$=$\frac{1}{3}$,
∴tanα=2$\sqrt{2}$,
由抛物线的对称性可知当A在第四象限时,tanα=-2$\sqrt{2}$.
∴直线AB的斜率为±2$\sqrt{2}$.
故选:B.
点评 本题考查抛物线的定义,考查直线的斜率的计算,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C:x2=4y,直线l1与C相交于A,B两点,线段AB与它的中垂线l2交于点G(a,1)(a≠0).
如图,已知抛物线C:x2=4y,直线l1与C相交于A,B两点,线段AB与它的中垂线l2交于点G(a,1)(a≠0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪[$\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$] | C. | [$\frac{1}{e}$,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com