
分析 (1)函数图象开口向上,对称轴x=2,故f(x)在[0,1]递减;进而根据在区间[0,1]上有最大值1和最小值-2,可得a,b的值;
(2)若在区间[-1,1]上,不等式f(x)>-x+m恒成立,函数g(x)=x2-3x+1-m在[-1,1]上的最小值大于0,进而可得实数m的取值范围.
解答 解:(1)f(x)=a(x2-4x)+b=a(x-2)2+b-4a
∵a>0,
∴函数图象开口向上,对称轴x=2,
∴f(x)在[0,1]递减;
∴f(0)=b=1,且f(1)=b-3a=-2,
∴a=b=1;
(2)f(x)>-x+m等价于x2-4x+1>-x+m,
即x2-3x+1-m>0,要使此不等式在[-1,1]上恒成立,
只需使函数g(x)=x2-3x+1-m在[-1,1]上的最小值大于0即可.
∵g(x)=x2-3x+1-m在[-1,1]上单调递减,
∴g(x)min=g(1)=-m-1,由-m-1>0得,m<-1.
因此满足条件的实数m的取值范围是(-∞,-1).
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
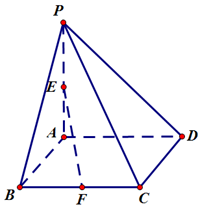 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com