
| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |
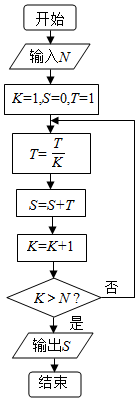
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:模拟程序的运行,可得
N=2016,K=1,S=0,T=1
执行循环体,T=1,S=1,K=2
不满足条件K>2016,执行循环体,T=$\frac{1}{2}$,S=1+$\frac{1}{2}$,K=3
不满足条件K>2016,执行循环体,T=$\frac{1}{2×3}$,S=1+$\frac{1}{2}$+$\frac{1}{2×3}$,K=4
不满足条件K>2016,执行循环体,T=$\frac{1}{2×3×4}$,S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{2×3×4}$,K=5
…
不满足条件K>2016,执行循环体,T=$\frac{1}{2×3×4×…×2015}$,S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+…+$\frac{1}{2×3×4×…×2015}$,K=2016
不满足条件K>2016,执行循环体,T=$\frac{1}{2×3×…×2016}$,S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+…+$\frac{1}{2×3×4×…×2015}$+$\frac{1}{2×3×…×2016}$,K=2017
满足条件K>2016,退出循环,输出S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+…+$\frac{1}{2×3×4×…×2015}$+$\frac{1}{2×3×…×2016}$=1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$,
故选:D.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | ($\frac{1}{2}$,+∞}) | C. | ($\sqrt{2}$,+∞) | D. | ($\frac{{\sqrt{2}}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x-y+3=0 | C. | x+3y-7=0 | D. | 3x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,该程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输出的a=3,则输入的a,b分别可能为( )
如图,该程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输出的a=3,则输入的a,b分别可能为( )| A. | 15、18 | B. | 14、18 | C. | 13、18 | D. | 12、18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com