
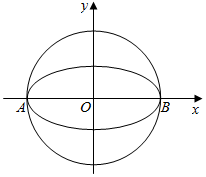
 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.分析 (Ⅰ)由A在圆上,可得a=4,再由离心率公式,可得c,结合a,b,c的关系,可得b,进而得到椭圆方程;
(Ⅱ)求得圆心到直线的距离,运用圆的弦长公式可得|QA|,化简整理,即可判断是否存在.
解答 解:(Ⅰ)因为椭圆W的左顶点A在圆O:x2+y2=16上,所以a=4.
又离心率为$\frac{{\sqrt{3}}}{2}$,所以$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,所以$c=2\sqrt{3}$,
则b2=a2-c2=4,所以W的方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.
(Ⅱ)设直线AP的方程为y=k(x+4),
代入椭圆方程可得(1+4k2)x2+32k2x+64k2-16=0,
由-4xP=$\frac{64{k}^{2}-16}{1+4{k}^{2}}$,可得xP=$\frac{4-16{k}^{2}}{1+4{k}^{2}}$,
即有|AP|=$\frac{8}{1+4{k}^{2}}$,
圆心到直线AP的距离为$d=\frac{|4k|}{{\sqrt{{k^2}+1}}}$,
所以$|AQ|=2\sqrt{16-{d^2}}=2\sqrt{\frac{16}{{1+{k^2}}}}=\frac{8}{{\sqrt{1+{k^2}}}}$.
因为$\frac{|PQ|}{|AP|}=\frac{|AQ|-|AP|}{|AP|}=\frac{|AQ|}{|AP|}-1$,
代入得到$\frac{|PQ|}{|AP|}=\frac{{\frac{8}{{\sqrt{1+{k^2}}}}}}{{\frac{{8\sqrt{1+{k^2}}}}{{1+4{k^2}}}}}-1=\frac{{1+4{k^2}}}{{1+{k^2}}}-1=\frac{{3{k^2}}}{{1+{k^2}}}=3-\frac{3}{{1+{k^2}}}$.
显然$3-\frac{3}{{1+{k^2}}}≠3$,
所以不存在直线AP,使得$\frac{|PQ|}{|AP|}=3$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查存在性问题的解法,注意运用点到直线的距离公式和弦长公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-$\frac{1}{2}$,2] | C. | [-1,2] | D. | [-$\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
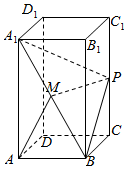 如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36或4 | B. | 6 | C. | $2\sqrt{21}$ | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4k+1,4k+3](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [2k+1,2k+2](k∈Z) | D. | [2k-1,2k+2](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com