
【题目】已知![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值,并写出
的值,并写出![]() 在区间
在区间![]() 上的增减性和值域(不需要证明);
上的增减性和值域(不需要证明);
(2)令![]() ,其中
,其中![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)令![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,在
,在![]() 上是增函数,值域为
上是增函数,值域为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用偶函数的定义![]() ,作差变形可求出
,作差变形可求出![]() ,结合函数
,结合函数![]() 的解析式写出该函数在区间
的解析式写出该函数在区间![]() 上的单调性,并利用单调性得出函数
上的单调性,并利用单调性得出函数![]() 在该区间上的值域;
在该区间上的值域;
(2)由题意得出![]() ,且
,且![]() ,换元
,换元![]() ,构造函数
,构造函数![]() ,由
,由![]() 可得出二次函数
可得出二次函数![]() 的对称轴
的对称轴![]() ,分析函数
,分析函数![]() 在区间
在区间![]() 上的单调性,求出函数
上的单调性,求出函数![]() 的最大值和最小值,结合不等式
的最大值和最小值,结合不等式![]() 求出实数
求出实数![]() 的取值范围;
的取值范围;
(3)由![]() 可得出
可得出![]() ,求出不等式右边代数式的取值范围,可得出实数
,求出不等式右边代数式的取值范围,可得出实数![]() 的取值范围.
的取值范围.
(1)![]() 函数
函数![]() 为偶函数,则
为偶函数,则![]() ,
,
即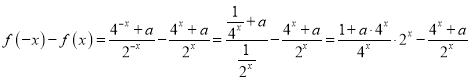
![]() ,
,
由题意知,对任意的![]() ,
,![]() 恒成立,则
恒成立,则![]() ,
,![]() ,
,
![]() ,该函数在区间
,该函数在区间![]() 上为增函数,且
上为增函数,且![]() ,
,
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
(2)由题意知,![]() ,且
,且![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,且
,且![]() ,
,
设函数![]() ,则
,则![]() ,二次函数
,二次函数![]() 的对称轴为直线
的对称轴为直线![]() .
.
![]() ,
,![]() ,则函数
,则函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
由![]() ,
,
可得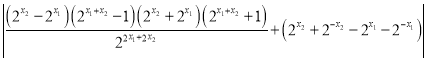
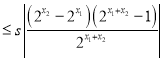 ,
,
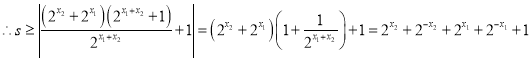 ,
,
由于函数![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,![]() ,
,
![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,
所以,![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某市小型机动车驾照“科二”考试中共有5项考察项目,分别记作①,②,③,④,⑤.
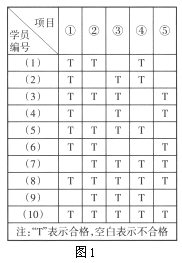
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如图1所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3项的概率;
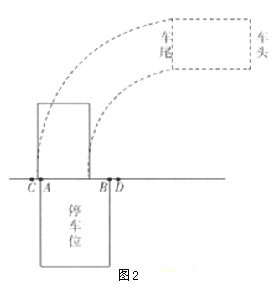
(2)如图2,某次模拟演练中,教练要求学员甲倒车并转向90°,在汽车边缘不压射线AC与射线BD的前提下,将汽车驶入指定的停车位. 根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD,且位于CD内各处的机会相等.若CA="BD=0.3m," AB="2.4m." 汽车宽度为1.8m, 求学员甲能按教练要求完成任务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()

①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为![]() (
(![]() )件.当
)件.当![]() 时,年销售总收人为(
时,年销售总收人为(![]() )万元;当
)万元;当![]() 时,年销售总收人为
时,年销售总收人为![]() 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为![]() 万元.(年利润=年销售总收入一年总投资)
万元.(年利润=年销售总收入一年总投资)
(1)求![]() (万元)与
(万元)与![]() (件)的函数关系式;
(件)的函数关系式;
(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国际性会议纪念章的一特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向该会议的组织委员会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时,该店一年可销售2000枚,经过市场调研发现,每枚纪念章的销售价格在每枚20元的基础上,每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元(每枚的销售价格应为正整数).
元(每枚的销售价格应为正整数).
(1)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式;
的函数关系式;
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值;
(元)最大,并求出这个最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com