
分析 (1)求出f(x)的导数,求得切线的斜率,解方程可得m;
(2)f(x)>g(x)即为ex+m>ln(x+1)+2.由函数y=ex-x-1,求得最小值,可得ex≥x+1,则ex+m>x+m+1,再由h(x)=x+m+1-ln(x+1)-2=x+m-ln(x+1)-1,求出导数,求得最小值,由条件即可得证.
解答 解:(1)函数f(x)=ex+m-x3的导数为f′(x)=ex+m-3x2,
在点(0,f(0))处的切线斜率为k=em=e,
解得m=1;
(2)证明:m≥l 时,f(x)>g(x)即为
ex+m>ln(x+1)+2.
由y=ex-x-1的导数为y′=ex-1,
当x>0时,y′>0,函数递增;当x<0时,y′<0,函数递减.
即有x=0处取得极小值,也为最小值0.
即有ex≥x+1,则ex+m≥x+m+1,
由h(x)=x+m+1-ln(x+1)-2=x+m-ln(x+1)-1,
h′(x)=1-$\frac{1}{x+1}$,当x>0时,h′(x)>0,h(x)递增;
-1<x<0时,h′(x)<0,h(x)递减.
即有x=0处取得最小值,且为m-1,
当m≥1时,即有h(x)≥m-1≥0,
即x+m+1≥ln(x+1)+2,
则有f(x)>g(x)成立.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式的证明,注意运用构造法,以及不等式的传递性,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{{m}^{2}}$$+\frac{{y}^{2}}{{n}^{2}}$=1 | B. | $\frac{{x}^{2}}{{n}^{2}}$$+\frac{{y}^{2}}{{m}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{m}^{2}}$$+\frac{{y}^{2}}{{m}^{2}-{n}^{2}}$=1 | D. | $\frac{{x}^{2}}{{m}^{2}-{n}^{2}}$$+\frac{{y}^{2}}{{n}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,19] | B. | [$-\frac{1}{5},3$] | C. | [$-\frac{1}{5},0$] | D. | [$-\frac{1}{5},19$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1+k}$ | B. | $\frac{1}{k}$ | C. | $\frac{1}{{e({1+k})}}$ | D. | $\frac{e}{1+k}$ |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,△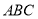 是圆
是圆 的内接三角形,
的内接三角形, 是
是 的延长线上一点,且
的延长线上一点,且 切圆
切圆 于点
于点 .
.

(1)求证: ;
;
(2)若 ,且
,且 ,求
,求 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com