练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线C的极坐标方程是ρ＝2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为(t为参数).

    (1)写出直线l的普通方程与曲线C的直角坐标方程;

    (2)设曲线C经过伸缩变换得到曲线,设M(x,y)为上任意一点,求的最小值,并求相应的点M的坐标.

    【答案】（1）， ；（2）当M为或时原式取得最小值1.

    【解析】试题分析：(1)将直线中的参数消去，即可得到其普通方程，在极坐标方程两边平方，由替换即可得到圆的直角坐标方程．(2)由变换公式先写出变换后的方程为一椭圆，用椭圆的参数方程表示点代入，由三角函数知识求之即可．

    试题解析：（1）由，得，代入，

    得直线的普通方程．

    由，得，∴．

    （2）∵，∴的直角坐标方程为．

    ∴设，则．

    ∴．

    ∴当，即或，上式取最小值．

    即当或， 的最小值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列和满足若为等比数列，且

    （1）求和；

    （2）设，记数列的前项和为

    ①求；

    ②求正整数 k，使得对任意均有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义平面向量之间的一种运算“⊙”如下：对任意的 ，令 ，下面说法错误的是（ ）
    A.若 与 共线，则 ⊙ =0
    B. ⊙ = ⊙
    C.对任意的λ∈R，有 ⊙ = ⊙ ）
    D.（ ⊙ ）2+（ ）2=| |2| |2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知极坐标系的极点为直角坐标系的原点，极轴为轴的正半轴，两种坐标系中的长度单位相同，圆的直角坐标方程为，直线的参数方程为（为参数），射线的极坐标方程为．

    （1）求圆和直线的极坐标方程；

    （2）已知射线与圆的交点为，与直线的交点为，求线段的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一汽车厂生产三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）：

    轿车

    轿车

    轿车

    舒适型

    100

    150

    标准型

    300

    450

    600

    按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有类轿车10辆．

    （I）求的值；

    （II）用分层抽样的方法在类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；

    （III）用随机抽样的方法从类舒适型轿车中抽取8辆，经检测它们的得分的值如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2，把这8辆轿车的得分看成一个总体，从中任取一个数，设样本平均数为，求的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= +
    （1）将函数f（x）化简成Asin（ωx+φ）+B（A＞0，φ＞0，φ∈[0，2π））的形式；
    （2）求f（x）的单调递减区间，并指出函数|f（x）|的最小正周期；
    （3）求函数f（x）在[ ， ]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，A=30°，BC=2 ，D是AB边上的一点，CD=2，△BCD的面积为4，求AC的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】利用简单随机抽样从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图如图所示．在这些用户中，用电量落在区间[150，250]内的户数为（ ）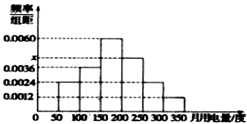

    A.46
    B.48
    C.50
    D.52

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数

    （1）求不等式的解集；

    （2）若，求证： .

    查看答案和解析>>

    同步练习册答案