Question

6．已知定义域为R的奇函数f（x）满足：当x＞0时，f（x）=lnx，则函数g（x）=f（x）-sin4x的零点的个数为7．

Answer 1

分析 将函数g（x）=f（x）-sin4x的零点的个数转化为f（x）的图象与sin4x的图象的交点个数，由数形结合可以得知答案．

解答 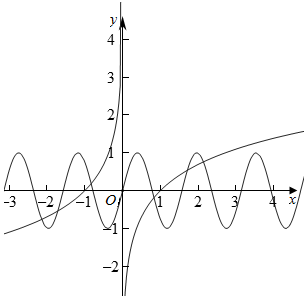解：函数f（x）=sin4x是奇函数，且它的周期为 $\frac{2π}{4}$=$\frac{π}{2}$，
∵g（x）=f（x）-sin4x=0，
∴函数g（x）=f（x）-sin4x的零点的个数为
相当于f（x）=sin4x的零点个数，
即f（x）与sin4x的交点个数，
∴画出二者图象，由数形结合，
可知，在（-∞，0）有3个交点，0处有一个交点，（0，+∞）有3个交点，
故共有7个交点．
∴函数g（x）=f（x）-sin4x的零点的个数为7个，
故答案为：7．

点评 本题考查数形结合的思想，考查学生灵活转化题目条件的能力，属于中档题．