
已知函数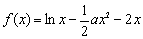 (
(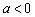 ).
).
(Ⅰ)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)若 ,且关于
,且关于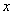 的方程
的方程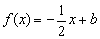 在
在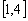 上恰有两个不等的实根,
上恰有两个不等的实根,
求实数 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列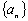 满足
满足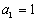 ,
,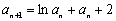 (
(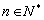 ),
),
求证: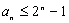 .
.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
函数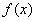 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间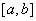
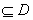 ,使得函数
,使得函数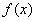 满足:
满足:
(1)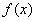 在
在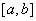 内是单调函数;(2)
内是单调函数;(2)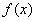 在
在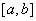 上的值域为
上的值域为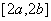 ,则称区间
,则称区间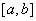 为函数
为函数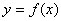 的“和谐区间”。下列函数中存在“和谐区间”的是 .
的“和谐区间”。下列函数中存在“和谐区间”的是 .
①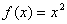 ,
, ②
②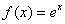 ,
,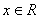
③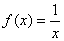 ,
, ④
④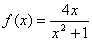 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数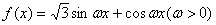 的图象与
的图象与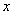 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为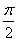 的等差数列,把函数
的等差数列,把函数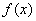 的图象沿
的图象沿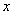 轴向左平移
轴向左平移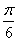 个单位,得到函数
个单位,得到函数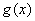 的图象.关于函数
的图象.关于函数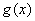 ,下列说法正确的是
,下列说法正确的是
A. 在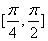 上是增函数 B. 其图象关于直线
上是增函数 B. 其图象关于直线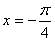 对称
对称
C. 函数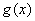 是奇函数 D. 当
是奇函数 D. 当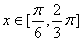 时,函数
时,函数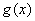 的值域是
的值域是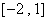
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗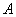 原料1千克、
原料1千克、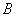 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗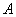 原料2千克,
原料2千克,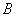 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗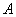 、
、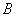 原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com