
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 114 | 106 | 115 | 77 | 86 | 90 | 95 | 86 | 97 | 79 | 100 | 78 | 77 | 113 | 60 |
| 物理成绩 | 72 | 49 | 51 | 29 | 57 | 49 | 62 | 22 | 63 | 29 | 42 | 21 | 37 | 46 | 21 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 89 | 74 | 82 | 95 | 64 | 87 | 56 | 65 | 43 | 64 | 64 | 85 | 66 | 56 | 51 |
| 物理成绩 | 65 | 45 | 33 | 28 | 29 | 28 | 39 | 34 | 45 | 35 | 35 | 34 | 20 | 29 | 39 |
| 物理Ⅰ | 物理Ⅱ | 合计 | |
| 数学Ⅰ | 4 | ||
| 数学Ⅱ | 15 | ||
| 合计 | 30 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据考试成绩填写列联表,利用公式计算K2,根据所给参数即可得出结论;
(2)由题意知ξ满足超几何分布,计算对应的概率,写出ξ的分布列与数学期望值.
解答 解:(1)根据这次考试的成绩填写2×2列联表,如下;
| 物理Ⅰ | 物理Ⅱ | 合计 | |
| 数学Ⅰ | 4 | 11 | 15 |
| 数学Ⅱ | 0 | 15 | 15 |
| 合计 | 4 | 26 | 30 |
| ξ | 0 | 1 | 2 |
| P(ξ) | $\frac{65}{87}$ | $\frac{104}{435}$ | $\frac{2}{145}$ |
点评 本题考查了独立性检验与离散型随机变量的分布列与期望的计算问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.
点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 108 | B. | 96 | C. | 120 | D. | 112 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
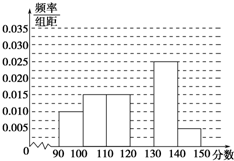 某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:| 数学成绩“优秀” | 数学成绩“一般” | 总计 | |
| 地理成绩“优秀” | 10 | 40 | 50 |
| 地理成绩“一般” | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com