
���� �٢���Ҫ�ǵ�a��b���ʱ�������
�ڢۿ�������ȽϷ��ж����ó����ۣ�
��� �⣺�١�a��b��0�����Ƴ���$\frac{1}{a}$��$\frac{1}{b}$��������֮��һ��������a��0ʱ�����������dz�ֲ���Ҫ����������ȷ��
��a��b��0��t��0����$\frac{a}{b}$-$\frac{a+t}{b+t}$=$\frac{t��a-b��}{b��b+t��}$��0����$\frac{a}{b}$��$\frac{a+t}{b+t}$���ʴ���
��a5+b5-a2b3+a3b2=��a-b��2��a+b����a2+ab+b2������Ȼ��һ����ʵ��a��b������������ȷ��
�ܡ�$\frac{a}{b}$��1���Ʋ�����a-b��0������֮Ҳ���ܣ�Ӧ�Ǽ������Ҳ����Ҫ�������ʴ���
�ʴ�Ϊ�٢ۣ�
���� �����������Ĺ�ϵ�������Ӧ�ã����ڻ������ͣ�Ӧ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
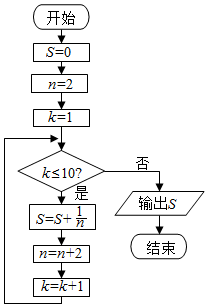
| A�� | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+��+$\frac{1}{11}$ | B�� | $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+��+$\frac{1}{22}$ | C�� | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+��+$\frac{1}{10}$ | D�� | $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+��+$\frac{1}{20}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{5��}{6}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
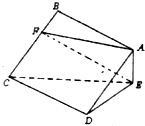 ��֪�߳�Ϊ2��������ABCD���ڵ�ƽ�����CDE����ƽ�潻��CD����AE��ƽ��CDE��AE=1��
��֪�߳�Ϊ2��������ABCD���ڵ�ƽ�����CDE����ƽ�潻��CD����AE��ƽ��CDE��AE=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com