
| A. | f(a)+f(b)≤0 | B. | f(a)+f(b)≥0 | C. | f(a)-f(b)≤0 | D. | f(a)-f(b)≥0 |
分析 求解函数f(x)的定义域,判断其奇偶性和单调性,利用奇偶性和单调性可得答案.
解答 解:设$f(x)={x^3}+{log_2}(x+\sqrt{{x^2}+1})$,其定义域为R,
$f(-x)={-x^3}+{log_2}(-x+\sqrt{{x^2}+1})$=$-{x}^{3}-lo{g}_{2}(x+\sqrt{{x}^{2}+1})$=-f(x),
∴函数f(x)是奇函数.且在(0,+∞)上单调递增,
故函数f(x)在R上是单调递增,
那么:a+b≥0,即a≥-b,
∴f(a)≥f(-b),
得f(a)≥-f(b),
可得:f(a)+f(b)≥0.
故选:B.
点评 本题考查了函数的奇偶性和单调性的判断及其运用能力.属于基础题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | a |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | $4\sqrt{3}$ | D. | $8\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
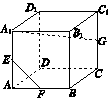 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com