
分析 ①根据双曲线的定义知①不正确;
②设出定圆的方程,利用代入法分析可知AB中点P的轨迹为圆(除去A点);
③求出双曲线的焦点与椭圆的焦点,即可判定;
④双曲线的离心率大于1,椭圆的离心率小于1大于0,即可判定.;⑤说明点(2,1)在直线3x+4y-10=0上,不满足抛物线的定义.
解答 解:①平面内与两个定点F1,F2的距离的差的绝对值等于常数k(k<|F1F2|)的点的轨迹叫做双曲线,当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,∴①不正确;
②,设定圆C的方程为x2+y2+Dx+Ey+F=0,点A(m,n),P(x,y),由$\overrightarrow{OP}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$可知P为AB的中点,则B(2x-m,2y-n),因为AB为圆的动弦,所以B在已知圆上,把B的坐标代入圆x2+y2+Dx+Ey+F=0得到P的轨迹仍为圆,当B与A重合时AB不是弦,所以点A除外,所以②不正确;
③双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1$与椭圆$\frac{{x}^{2}}{35}+{y}^{2}=1$的焦点都是(±$\sqrt{34}$,0),有相同的焦点,正确;
④正确方程2x2-5x+a=0的可分别作为椭圆和双曲线的离心率,则$\left\{\begin{array}{l}{a>0}\\{2-5+a<0}\end{array}\right.$,∴0<a<3,正确;
⑤在平面内,点(2,1)在直线3x+4y-10=0上,
∴到定点(2,1)的距离与到定直线3x+4y-10=0的距离相等的点的轨迹不是抛物线,∴⑤不正确
故答案为:③④.
点评 本题通过命题真假的判定,考查椭圆、双曲线抛物线的定义、性质和曲线的方程与方程的曲线等问题,是综合题目.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
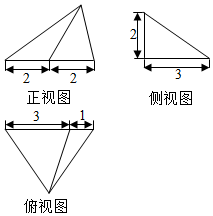
| A. | 4cm | B. | $\sqrt{13}$cm | C. | $\sqrt{14}$cm | D. | $\sqrt{15}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
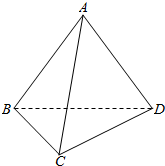
| A. | -2 | B. | 2 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com