
| A. | $\frac{5}{36}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
分析 记下的颜色中有红有白但没有黄的情况有两种:2红1白,1红2白,由此能求出所求概率.
解答 解:∵从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球,
摸到红球、白球和黄球的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,
从袋中随机摸出一个球,记下颜色后放回,连续摸3次,
∴记下的颜色中有红有白但没有黄的情况有两种:2红1白,1红2白,
则所求概率:
p=${C}_{3}^{1}×\frac{1}{2}×(\frac{1}{3})^{2}+{C}_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{3}$=$\frac{5}{12}$.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
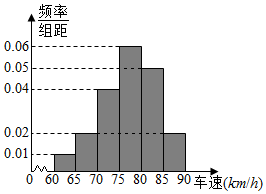 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )| A. | 75,0.25 | B. | 80,0.35 | C. | 77.5,0.25 | D. | 77.5,0.35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4) | D. | (1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com