
 已知梯形ABCD中,BC∥AD,AB=BC=$\frac{1}{2}$AD=1,且∠ABC=90°,以AC为折痕使得折叠后的图形中平面DAC⊥ABC.
已知梯形ABCD中,BC∥AD,AB=BC=$\frac{1}{2}$AD=1,且∠ABC=90°,以AC为折痕使得折叠后的图形中平面DAC⊥ABC.分析 (1)取AD的中点E,连CE,证明DC⊥AC,即可证明DC⊥平面ABC;
(2)确定四面体ABCD的外接球的球心是AD的中点E,即可求四面体ABCD的外接球的体积;
(3)利用反证法判断在棱AD上是否存在点P,使得AD⊥平面PBC.
解答 (1)证明:取AD的中点E,连CE,由条件可知四边形ABCE是正方形,
三角形CED是等腰直角三角形,∴∠ACD=∠ACE+∠ECD=45°+45°=90°
即DC⊥AC…(2分)
∵平面DAC⊥平面ABC,∴DC⊥平面ABC…(4分)
(2)解:∵DC⊥平面ABC,∴DC⊥AB
又∵AB⊥BC,BC∩DC=C,
∴AB⊥平面DBC,∴AB⊥DB,
即∠ABD=∠ACD=90°,∴四面体ABCD的外接球的球心是AD的中点E…(6分)
即四面体ABCD的外接球的半径R=1,故四面体ABCD的外接球的体积为$\frac{4π}{3}$…(8分)
(3)解:若在棱AD上存在点P,使得AD⊥平面PBC,则AD⊥BC,
又DC⊥平面ABC,∴DC⊥BC,∴BC⊥平面ADC…(10分)
从而BC⊥AC,这与∠ACB=45°矛盾
所以在棱AD上不存在点P,使得AD⊥平面PBC…(12分)
点评 本题考查平面与平面垂直的性质,考查线面垂直的判定,考查四面体ABCD的外接球的体积,考查学生分析解决问题的能力,属于中档题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
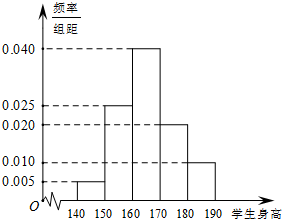 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com