
已知函数f(x)=|x+1|+|x-2|-m.
(1)当m=5时,求f(x)>0的解集;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
已知曲线C1:ρ=2sinθ,曲线C2: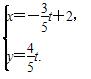 (t为参数).
(t为参数).
(1)化C1为直角坐标方程,化C2为普通方程;
(2)若M为曲线C2与x轴的交点,N为曲线C1上一动点,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|x+1|+|x-3|.
(1)作出函数y=f(x)的图象;
(2)若对任意x∈R,f(x)≥a2-3a恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题:“在等差数列{an}中,若4a2+a10+a( )=24,则S11为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
国家法定工作日内,每周工作时间满工作量为40h,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为xh,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y元的算法的流程图.(注:满工作量外的工作时间为加班)
查看答案和解析>>
科目:高中数学 来源: 题型:
设z1,z2是复数,则下列命题中的假命题是( )
A.若|z1-z2|=0,则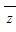 1=
1=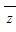 2
2
B.若z1=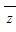 2,则
2,则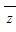 1=z2
1=z2
C.若|z1|=|z2|,则z1·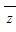 1=z2·
1=z2·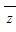 2
2
D.若|z1|=|z2|,则z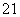 =z
=z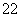
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com