
已知曲线C1:ρ=2sinθ,曲线C2: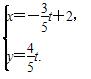 (t为参数).
(t为参数).
(1)化C1为直角坐标方程,化C2为普通方程;
(2)若M为曲线C2与x轴的交点,N为曲线C1上一动点,求|MN|的最大值.
科目:高中数学 来源: 题型:
已知f(n)=1+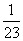 +
+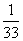 +
+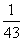 +…+
+…+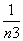 ,g(n)=
,g(n)=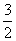 -
-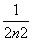 ,n∈N*.
,n∈N*.
(1)当n=1,2,3时,试比较f(n)与g(n)的大小;
(2)猜想f(n)与g(n)的大小关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
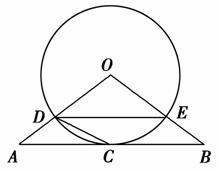
(1)求证:直线AB是⊙O的切线;
(2)若AD=2,且tan∠ACD=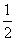 ,求⊙O的半径r的长.
,求⊙O的半径r的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线C1: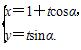 (t为参数),圆C2:ρ=1.(极坐标轴与x轴非负半轴重合)
(t为参数),圆C2:ρ=1.(极坐标轴与x轴非负半轴重合)
(1)当α=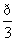 时,求直线C1被圆C2所截得的弦长;
时,求直线C1被圆C2所截得的弦长;
(2)过坐标原点O作C1的垂线,垂足为A.当a变化时,求A点的轨迹的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标坐标系取相等的单位长度.已知直线l经过点P(1,1),倾斜角α=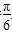 .
.
(1)写出直线l的参数方程;
(2)设l与圆ρ=2相交于两点A、B,求点P到A、B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M={x||2x-1|<2},N=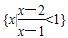 ,则M∩N等于( )
,则M∩N等于( )
A.{x|1<x<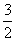 } B.{x|
} B.{x| <x<1}
<x<1}
C.{x|- <x<
<x<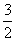 } D.{x|-
} D.{x|- <x<
<x<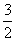 ,且x≠1}
,且x≠1}
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|x+1|+|x-2|-m.
(1)当m=5时,求f(x)>0的解集;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列程序的功能是:
判断任意输入的数x是否是正数,若是,输出它的平方值;若不是,输出它的相反数.
输入x
If________Then
y=-x;
else
y=x*x
end If
输出y
则填入的条件应该是( )
A.x>0 B.x<0
C.x>=0 D.x<=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com