练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知不等式≥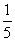|a2－a|对于x∈[2,6]恒成立，则实数a的取值范围是________．


    [－1,2]

    [解析]　设y＝，x∈[2,6]，则y′＝－<0，则y＝在区间[2,6]上单调递减，则ymin＝＝，故不等式≥|a2－a|对于x∈[2,6]恒成立等价于|a2－a|≤成立，等价于解得－1≤a≤2，故a的取值范围是[－1,2]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，四边形ABCD中，DF⊥AB，垂足为F，DF＝3，AF＝2FB＝2，延长FB到E，使BE＝FB，连接BD，EC.若BD∥EC，则四边形ABCD的面积为(　　)

    A．4                                                             B．5 

    C．6                                                             D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设曲线C的参数方程为(t为参数)，若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知曲线C1：ρ＝2sinθ，曲线C2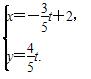：(t为参数)．

    (1)化C1为直角坐标方程，化C2为普通方程；

    (2)若M为曲线C2与x轴的交点，N为曲线C1上一动点，求|MN|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{x||x－a|<1，x∈R}，B＝{x||x－b|>2，x∈R}．若A⊆B，则实数a、b必满足(　　)

    A．|a＋b|≤3                                                 B．|a＋b|≥3

    C．|a－b|≤3                                                 D．|a－b|≥3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|x＋1|＋|x－3|.

    (1)作出函数y＝f(x)的图象；

    (2)若对任意x∈R，f(x)≥a2－3a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a、b、c均为正数，且a＋b＋c＝1，证明：

    (1)ab＋bc＋ac≤；

    (2)＋＋≥1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题：“在等差数列{an}中，若4a2＋a10＋a(　)＝24，则S11为定值”为真命题，由于印刷问题，括号处的数模糊不清，可推得括号内的数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若z＝，则复数＝(　　)

    A．－2－i                                                     B．－2＋i

    C．2－i                                                         D．2＋i

    查看答案和解析>>

    同步练习册答案