练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．若集合M={x||x|≤1}，N={y|y=x2，|x|≤1}，则（　　）
    A．M=NB．M⊆NC．N⊆MD．M∩N=∅

    分析 化简N，即可得出结论．

    解答 解：由题意，N={y|y=x2，|x|≤1}={y|0≤y≤1}，
    ∴N⊆M，
    故选C．

    点评 本题考查集合的化简，考查集合的关系，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

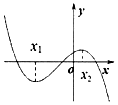
    4．函数f（x）=ax3+bx2+cx+d的图象如图所示，则下列结论成立的是（　　）
    A．a＞0，b＞0，c＞0，d＜0B．a＞0，b＞0，c＜0，d＜0C．a＜0，b＜0，c＞0，d＞0D．a＞0，b＞0，c＞0，d＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设数列{an}满足a1=a，an+1=$\frac{a_n^2-2}{{{a_n}+1}}$（n∈N），若数列{an}是常数列，则a=（　　）
    A．-2B．-1C．0D．（-1）n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知角α的顶点在坐标原点，始边与x轴的非负半轴重合，终边经过点（-$\sqrt{3}$，2），则tan（α-$\frac{π}{6}$）的值为（　　）
    A．-3$\sqrt{3}$B．-$\frac{\sqrt{3}}{5}$C．-$\frac{5\sqrt{3}}{3}$D．-$\frac{3\sqrt{3}}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知{an}是等差数列，其前n项和为Sn，a1+a3+a5=15，a2+a4+a6=0，则Sn的最大值为30．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知p：?x＞0，ex-ax＜1成立，q：函数f（x）=-（a-1）x是减函数，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知复数z的实部为-1，虚部为2，则$\frac{5i}{\overline z}$对应的点位于（　　）
    A．第四象限B．第一象限C．第三象限D．第二象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲，乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在（195，210]内，则为合格品，否则为不合格品．表1是甲流水线样本的频数分布表，如图是乙流水线样本的频率分布直方图．
    甲流水线样本的频数分布表
    质量指标值频数
    （190，195]9
    （195，200]10
    （200，205]17
    （205，210]8
    （210，215]6
    （Ⅰ）根据图1，估计乙流水线生产产品该质量指标值的中位数；
    （Ⅱ）若将频率视为概率，某个月内甲，乙两条流水线均生产了5000件产品，则甲，乙两
    条流水线分别生产出不合格品约多少件？
    （Ⅲ）根据已知条件完成下面2×2列联表，并回答是否有85%的把握认为“该企业生产的这
    种产品的质量指标值与甲，乙两条流水线的选择有关”？
    甲生产线乙生产线合计
    合格品
    不合格品
    合计
    附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若数据x1，x2，…，xn的平均值为$\overline x$，方差为S2，则3x1+5，3x2+5，…，3xn+5的平均值和方差分别为（　　）
    A．$\overline{x}$和S2B．3$\overline{x}$+5和9S2C．3$\overline{x}$+5和S2D．$\overline{x}$和9S2

    查看答案和解析>>

    同步练习册答案