练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．下面的程序段结果是（　　）
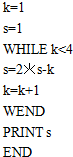
    A．-3B．-10C．0D．-2

    分析 遇到WHILE语句，先判断条件是否成立，如果成立，则执行WHILE和WEND之间的循环体，然后返回到WHILE语句再判断上述条件是否成立，如果成立，再执行循环体，这个过程反复执行，直到一次返回到WHILE语句判断上述条件不成立为止，这时不再执行循环体，而是跳到WEND语句后，从而输出结果．

    解答 解：模拟程序的运行，可得
    k=1，s=1
    满足条件k＜4，执行循环体，s=1，k=2
    满足条件k＜4，执行循环体，s=0，k=3
    满足条件k＜4，执行循环体，s=-3，k=4
    不满足条件k＜4，退出循环，输出s的值我-3．
    故选：A．

    点评 本题主要考查了伪代码的应用，解题的关键是根据题设中代码得出变量的运算方法，规律，计算出结果，这是近几年算法考试的主要方式，一般以框图告诉题面，如本题这样以代码告诉题目不多见，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．设a0为常数，且an=3n-1-2an-1（n∈N+），求an．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知复数z=$\frac{1-i}{1+i}$，求z4+2z3的虚部．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知M?{a，b，c}，则符合条件的M的个数是（　　）
    A．5B．6C．7D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$与双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点相同，且椭圆上任意一点到其两个焦点的距离之和为20，则椭圆的离心率e的值为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{7}}}{10}$C．$\frac{{\sqrt{7}}}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的两焦点F1，F2，若M是椭圆上一点，且满足∠F1MF2=60°，则离心率的范围是（　　）
    A．$[{\frac{1}{2}，1}）$B．$[{\frac{{\sqrt{3}}}{2}，1}）$C．$（{0，\frac{1}{2}}]$D．$（{0，\frac{{\sqrt{3}}}{2}}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知定义域为R的函数f（x）满足：①对任意的实数x，都有f（x+2）=2f（x）；②当x∈[-1，1]时，$f（x）=cos\frac{π}{2}x$．记函数g（x）=f（x）-log4（x+1），则函数g（x）在区间[0，10]内的零点个数是10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{1}{2}$，且过点$（{1，\frac{3}{2}}）$．若点M（x0，y0）在椭圆C上，则点$N（{\frac{x_0}{a}，\frac{y_0}{b}}）$称为点M的一个“椭点”．
    （I）求椭圆C的标准方程；
    （Ⅱ）若直线l：y=kx+m与椭圆C相交于A，B两点，且A，B两点的“椭点”分别为P，Q，以PQ为直径的圆经过坐标原点，试判断△AOB的面积是否为定值？若为定值，求出定值；若不为定值，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设函数f（x）在R上存在导函数f′（x），对?x∈R，f（-x）+f（x）=x2，且当x∈（0，+∞），f′（x）＞x，若有f（1-a）-f（a）≥$\frac{1}{2}$-a，则实数a的取值范围为（　　）（　　）
    A．（-∞，$\frac{1}{2}$]B．[$\frac{1}{2}$，+∞）C．（-∞，1]D．[1，+∞）

    查看答案和解析>>

    同步练习册答案