
| A. | 1 | B. | 2 | C. | 5 | D. | 6 |
分析 求得焦点坐标根据抛物线的定义可知:当F,P,D三点共线时丨PF丨+丨PD丨最小,求得DF的方程,代入抛物线方程,求得P点坐标,利用点到直线的距离公式即可求得P到直线l2的距离.
解答 解:由抛物线y2=16x焦点为(4,0),
由抛物线的定义可知:丨PC丨=丨PF丨,
P到直线l2的距离d为丨PD丨,
则丨PC丨+丨PD丨=丨PF丨+丨PD丨,
当F,P,D三点共线时丨PF丨+丨PD丨最小,最小值为丨FD丨=$\frac{丨12+0+18丨}{\sqrt{{3}^{2}+{4}^{2}}}$=6,
直线DF的斜率为$\frac{4}{3}$,DF的方程为:y=$\frac{4}{3}$(x-4),
$\left\{\begin{array}{l}{y=\frac{4}{3}(x-4)}\\{{y}^{2}=16x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=16}\\{y=16}\end{array}\right.$(舍去),
则P点坐标为(1,-4),
P到直线l2的距离d=$\frac{丨3×1+4×(-4)+18丨}{\sqrt{{3}^{2}+{4}^{2}}}$=1,
P到直线l2的距离1,
故选A.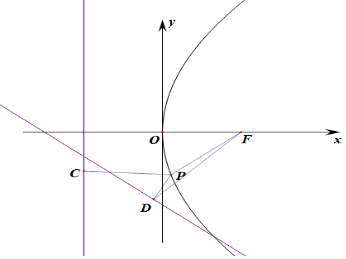
点评 本题考查抛物线的定义,直线与抛物线的位置关系,考查点到直线的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 60 | ||
| 不肥胖 | 10 | ||
| 合计 | 100 |
| P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$为平行向量 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$为模相等的向量 | ||
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$为共线向量 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$为相等的向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
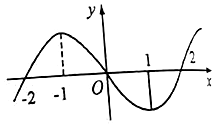 已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )
已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-∞,2)∪(2,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-2,-1)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
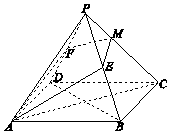 如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.
如图,在正四棱锥P-ABCD中,PA=AB,E,F分别为PB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 6 | 6 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com