
���� ��1��������1������������¼��ĸ��ʹ�ʽ���㼴�ɣ�
������2�����ùŵ���͵ĸ��ʹ�ʽ���㼴�ɣ�
��2�������⣬X��B��4��$\frac{1}{3}$��������n�ζ����ظ��¼��ĸ��ʹ�ʽ��
�����Ӧ�ĸ���ֵ��д����������εķֲ��У�������ѧ����ֵ��
��� �⣺��1��������1��ÿ�������ڡ����ء�Ƭ�������ֹ�˾�ĸ���Ϊ$\frac{1}{3}$��
ȥ��������Ƭ�������ֹ�˾�ĸ�����$\frac{2}{3}$��
����4������ǡ��2�����������ڡ����ء�Ƭ�������ֹ�˾�ĸ���Ϊ
P=${C}_{4}^{2}$��${��\frac{1}{3}��}^{2}$��${��1-\frac{1}{3}��}^{2}$=$\frac{8}{27}$��
������2�����п��ܵ����뷽ʽ��34=81�֣�
ǡ��2�����������ڡ����ء�Ƭ�������ֹ�˾�ķ�ʽΪ${C}_{4}^{2}$��22=24�֣�
�Ӷ�ǡ��2�������ڡ����ء�Ƭ�������ֹ�˾�ĸ���Ϊ��
P=$\frac{{C}_{4}^{2}{��2}^{2}}{{3}^{4}}$=$\frac{8}{27}$��
��2�������⣬X��B��4��$\frac{1}{3}$������
P��X=k��=${C}_{4}^{k}$•${��\frac{1}{3}��}^{k}$•${��1-\frac{1}{3}��}^{4-k}$��������k=0��1��2��3��4����
��ε����п���ȡֵΪ0��2��4��
P����=0��=P��X=2��=$\frac{8}{27}$��
P����=2��=P��X=1��+P��X=3��=$\frac{40}{81}$��
P����=4��=P��X=0��+P��X=4��=$\frac{17}{81}$��
������������εķֲ���Ϊ��
| �� | 0 | 2 | 4 |
| P | $\frac{8}{27}$ | $\frac{40}{81}$ | $\frac{17}{81}$ |
���� ���⿼����������¼��ĸ��ʹ�ʽ����ɢ����������ķֲ��к���ѧ������Ӧ�����⣬���е��⣮


 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{6}$��$\frac{5��}{6}$ | D�� | $\frac{��}{3}$��$\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|$\frac{1}{2}$��x��2} | B�� | {x|-1��x��0��$\frac{1}{2}$��x��2} | C�� | {x|-1��x��$\frac{1}{2}$} | D�� | {x|0��x��$\frac{1}{2}$��1��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
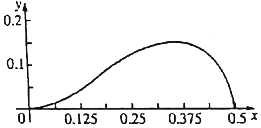 ����f��x��=axm��1-2x��n��a��0��������[0��$\frac{1}{2}$]�ϵ�ͼ����ͼ��ʾ����m��n��ֵ�����ǣ�������
����f��x��=axm��1-2x��n��a��0��������[0��$\frac{1}{2}$]�ϵ�ͼ����ͼ��ʾ����m��n��ֵ�����ǣ�������| A�� | m=1��n=1 | B�� | m=1��n=2 | C�� | m=2��n=3 | D�� | m=3��n=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[1-\sqrt{3}��+�ޣ�$ | B�� | [-2��+�ޣ� | C�� | $[-2��2\sqrt{2}]$ | D�� | $[-2��1+\sqrt{3}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\frac{{3\sqrt{2}}}{2}$ | D�� | $3\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com