
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | 2-$\sqrt{3}$ |
分析 由于|OF|为半焦距c,利用等边三角形性质,即可得点P的一个坐标,PF方程为:y=-$\sqrt{3}$(x-c)代入椭圆标准方程即可得N坐标,再用斜率公式,求解
解答 解:∵椭圆上存在点P使△AOF为正三角形,设F为左焦点,|OF|=c,P在第一象限,
∴点P的坐标为($\frac{c}{2},\frac{\sqrt{3}}{2}c$)代入椭圆方程得,$\frac{{c}^{2}}{4{a}^{2}}+\frac{{3c}^{2}}{4{b}^{2}}=1$.又因为a2=b2+c2,得到$c=(\sqrt{3}-1)a$.
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的方程可设为:2$\sqrt{3}$x2+(4+2$\sqrt{3}$)y2=(2$\sqrt{3}$+3)c2…①.
PF方程为:y=-$\sqrt{3}$(x-c)…②
由①②得N(($\sqrt{3}-\frac{1}{2}$)c,$\frac{3\sqrt{3}-6}{2}c$),
M,P两点关于原点对称,∴M(-$\frac{c}{2},-\frac{\sqrt{3}}{2}$c)
直线MN的斜率等于$\frac{\frac{3\sqrt{3}-6}{2}+\frac{\sqrt{3}}{2}}{\sqrt{3}}=2-\sqrt{3}$.
故选:D
点评 本题考查了椭圆与直线的位置关系,计算量较大,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{2}$,$\frac{2}{3}$] | B. | [-6,2] | C. | [-1,$\frac{7}{2}$] | D. | [-4,$\frac{2}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$] | C. | [1,$\sqrt{2}$] | D. | [$\frac{2\sqrt{3}}{3}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{{\sqrt{3}}}{3},1})$ | B. | $[{\frac{1}{3},\frac{1}{2}}]$ | C. | $[{\frac{{\sqrt{3}}}{3},\frac{{\sqrt{2}}}{2}})$ | D. | $({0,\frac{{\sqrt{2}}}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
在一个盒子里装有6张卡片,上面分别写着如下定义域为 的函数:
的函数:
 ,
,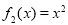 ,
,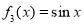 ,
,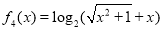 ,
, ,
,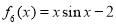 .
.
(1)现在从盒子中任意取两张卡片,记事件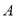 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件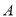 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为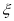 ,写出
,写出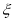 的分布列,并求其数学期望
的分布列,并求其数学期望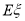 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com