
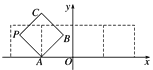
【题目】如图所示,放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:
有下列判断:
①若![]() ,则函数
,则函数![]() 是偶函数;
是偶函数;
②对任意的![]() ,都有
,都有![]() ;
;
③函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
其中判断正确的序号是________.(写出所有正确结论的序号)
【答案】①②④
【解析】
根据正方形的运动,得到点P的轨迹方程,然后根据函数的图象和性质分别进行判断即可.
当﹣2≤x≤﹣1,P的轨迹是以A为圆心,半径为1的![]() 圆,
圆,
当﹣1≤x≤1时,P的轨迹是以B为圆心,半径为![]() 的
的![]() 圆,
圆,
当1≤x≤2时,P的轨迹是以C为圆心,半径为1的![]() 圆,
圆,
当3≤x≤4时,P的轨迹是以A为圆心,半径为1的![]() 圆,
圆,
∴函数的周期是4.
因此最终构成图象如下:
①根据图象的对称性可知函数y=f(x)是偶函数,∴①正确.
②由图象即分析可知函数的周期是4.∴②正确.
③函数y=f(x)在区间[2,3]上单调递增,∴③错误.
④函数y=f(x)在区间[4,6]上是减函数,由函数的图象即可判断是真命题、∴④正确.
故答案为:①②④.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)某工厂八年来某种产品总产量y(即前x年年产量之和)与时间x(年)的函数关系如图,下列五种说法中正确的是( )
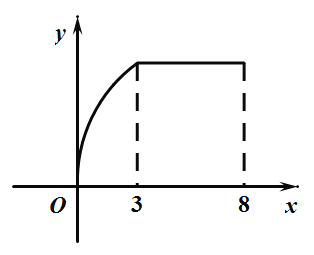
A.前三年中,总产量的增长速度越来越快
B.前三年中,总产量的增长速度越来越慢
C.前三年中,年产量的增长速度越来越慢
D.第三年后,这种产品停止生产
E.第三年后,年产量保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x-![]() -1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
-1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com