
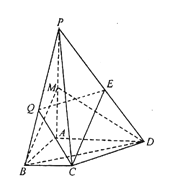
【题目】如图,在三棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() 为棱
为棱![]() 的中点,
的中点,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]()
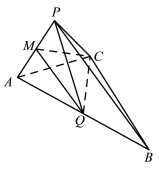
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 上一点,
上一点,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先根据平面![]() 平面
平面![]() ,得出
,得出![]() ,结合条件
,结合条件![]() 得出
得出![]() 平面
平面![]() ,从而可得.
,从而可得.
(2)建立空间直角坐标系,结合![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 得出
得出![]() 的坐标,然后利用法向量可求.
的坐标,然后利用法向量可求.
(1)因为![]() 为正三角形,
为正三角形,![]() 为棱
为棱![]() 的中点,所以
的中点,所以![]() ,
,
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)作![]() 中点
中点![]() ,连
,连![]() ,由(1)及
,由(1)及![]() 可知
可知![]() 平面
平面![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴,过
轴,过![]() 且平行于
且平行于![]() 的方向为
的方向为![]() 轴,如图,建立空间直角坐标系.
轴,如图,建立空间直角坐标系.
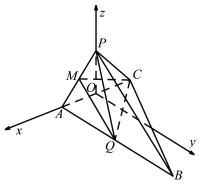
设![]() ,
,
则![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
即![]() 为
为![]() 的中点,则
的中点,则![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
 ,即
,即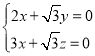 ,
,
取![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
则二面角![]() 的余弦值为
的余弦值为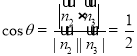 ,
,
故![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 中前两项
中前两项![]() 给定,若对于每个正整数
给定,若对于每个正整数![]() ,均存在正整数
,均存在正整数![]() (
(![]() )使得
)使得![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为
为![]() 的等比数列,当
的等比数列,当![]() 时,试问:
时,试问:![]() 与
与![]() 是否相等,并说明数列
是否相等,并说明数列![]() 是否为“
是否为“![]() 数列”;
数列”;
(2)讨论首项为![]() 、公差为
、公差为![]() 的等差数列
的等差数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(3)已知数列![]() 为“
为“![]() 数列”,且
数列”,且![]() ,记
,记![]() ,
,![]() ,其中正整数
,其中正整数![]() , 对于每个正整数
, 对于每个正整数![]() ,当正整数
,当正整数![]() 分别取1、2、
分别取1、2、![]() 、
、![]() 时
时![]() 的最大值记为
的最大值记为![]() 、最小值记为
、最小值记为![]() . 设
. 设![]() ,当正整数
,当正整数![]() 满足
满足![]() 时,比较
时,比较![]() 与
与![]() 的大小,并求出
的大小,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数,集合A=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(Ⅰ)当n=3时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)当![]() 时,对于
时,对于![]() 中的任意两个不同的元素
中的任意两个不同的元素![]() ,
,![]() ,证明:
,证明:![]() .
.
(Ⅲ)给定不小于2的正整数n,设B是A的子集,且满足:对于B中的任意两个不同元素![]() ,
,![]() ,
,![]() .写出一个集合B,使其元素个数最多,并说明由.
.写出一个集合B,使其元素个数最多,并说明由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
(1)求证:CE//平面BMD
(2)点Q为线段BP中点,求直线PA与平面CEQ所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种新的验血技术可以提高血液检测效率.现某专业检测机构提取了![]() 份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中
份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中![]() 份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这
份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这![]() 份血液再逐一检测,直到确定呈阳性的血液为止.
份血液再逐一检测,直到确定呈阳性的血液为止.
(1)若![]() ,求恰好经过3次检测而确定呈阳性的血液的事件概率;
,求恰好经过3次检测而确定呈阳性的血液的事件概率;
(2)若![]() ,宜采用以上方案检测而确定呈阳性的血液所需次数为
,宜采用以上方案检测而确定呈阳性的血液所需次数为![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将长方形OAA1O1(及其内部)绕OO1旋转一周形成圆柱,其中![]() ,弧
,弧![]() 的长为
的长为![]() ,AB为⊙O的直径.
,AB为⊙O的直径.
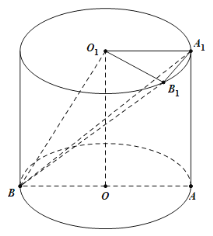
(1)在弧![]() 上是否存在点
上是否存在点![]() (
(![]() ,
,![]() 在平面
在平面![]() 的同侧),使
的同侧),使![]() ,若存在,确定其位置,若不存在,说明理由.
,若存在,确定其位置,若不存在,说明理由.
(2)求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com