解答:
解:(Ⅰ)由f(x)=2x
3-3x得f′(x)=6x
2-3,
令f′(x)=0得,x=-
或x=
,
∵f(-2)=-10,f(-
)=
,f(
)=-
,f(1)=-1,
∴f(x)在区间[-2,1]上的最大值为
.
(Ⅱ)设过点P(1,t)的直线与曲线y=f(x)相切于点(x
0,y
0),
则y
0=2
-3x
0,且切线斜率为k=6
-3,
∴切线方程为y-y
0=(6
-3)(x-x
0),
∴t-y
0=(6
-3)(1-x
0),
即4
-6
+t+3=0,
设g(x)=4x
3-6x
2+t+3,
则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,等价于“g(x)有3个不同的零点”.
∵g′(x)=12x
2-12x=12x(x-1),
∴g(x)与g′(x)变化情况如下:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | t+3 | ↘ | t+1 | ↗ |
∴g(0)=t+3是g(x)的极大值,g(1)=t+1是g(x)的极小值.
当g(0)=t+3≤0,即t≤-3时,g(x)在区间(-∞,1]和(1,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(1)=t+1≥0,即t≥-1时,g(x)在区间(-∞,0]和(0,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(0)>0且g(1)<0,即-3<t<-1时,∵g(-1)=t-7<0,g(2)=t+11>0,
∴g(x)分别在区间[-1,0),[0,1)和[1,2)上恰有1个零点,由于g(x)在区间(-∞,0)和[1,+∞)上单调,
故g(x)分别在区间(-∞,0)和[1,+∞)上恰有1个零点.
综上所述,当过点过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(-3,-1).
(Ⅲ)过点A(-1,2)存在3条直线与曲线y=f(x)相切;
过点B(2,10)存在2条直线与曲线y=f(x)相切;
过点C(0,2)存在1条直线与曲线y=f(x)相切.



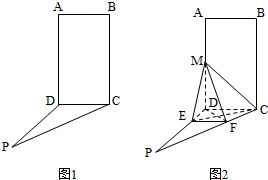 如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.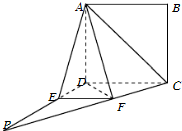 如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.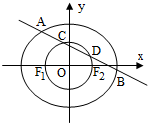 已知椭圆
已知椭圆 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.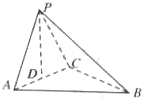 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4