
分析 (1)由$2t{\vec e_1}+7{\vec e_2}$与${\vec e_1}+t{\vec e_2}$的夹角为钝角,得($2t{\vec e_1}+7{\vec e_2}$)•(${\vec e_1}+t{\vec e_2}$)<0,且$2t{\vec e_1}+7{\vec e_2}≠λ({{{\vec e}_1}+t{{\vec e}_2}})({λ<0})$.展开得答案;
(2)直接利用向量在向量方向上的投影的概念求解.
解答 解:(1)$|{\vec e_1}|=2,|{\vec e_2}|=1$,且${\vec e_1}$与$\vec e$的夹角为60°,
∵$2t{\vec e_1}+7{\vec e_2}$与${\vec e_1}+t{\vec e_2}$的夹角为钝角,
∴($2t{\vec e_1}+7{\vec e_2}$)•(${\vec e_1}+t{\vec e_2}$)<0,且$2t{\vec e_1}+7{\vec e_2}≠λ({{{\vec e}_1}+t{{\vec e}_2}})({λ<0})$.
∴$2t{\overrightarrow{{e}_{1}}}^{2}+(2{t}^{2}+7)\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+7t{\overrightarrow{{e}_{2}}}^{2}$<0,且$2t{\vec e_1}+7{\vec e_2}≠λ({{{\vec e}_1}+t{{\vec e}_2}})({λ<0})$.
即$8t+(2{t}^{2}+7)×2×1×\frac{1}{2}+7t$<0,且$2t{\vec e_1}+7{\vec e_2}≠λ({{{\vec e}_1}+t{{\vec e}_2}})({λ<0})$.
解得:$-7<t<-\frac{1}{2}$且$t≠-\frac{{\sqrt{14}}}{2}$;
(2)$2{\vec e_1}+{\vec e_2}$在$3{\vec e_1}+2{\vec e_2}$方向上的投影为:
$\frac{(2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•(3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}})}{|3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}|}$=$\frac{6{\overrightarrow{{e}_{1}}}^{2}+2{\overrightarrow{{e}_{2}}}^{2}+7\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}{\sqrt{9{\overrightarrow{{e}_{1}}}^{2}+4{\overrightarrow{{e}_{2}}}^{2}+12\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}}$=$\frac{33\sqrt{13}}{26}$.
点评 本题考查平面向量的数量积运算,考查向量在向量方向上投影的概念,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
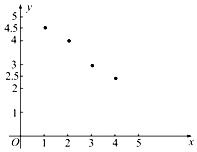 如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )
如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 10.5 | B. | 5.15 | C. | 5.2 | D. | 5.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [0,1] | C. | [0,1) | D. | [0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com