

���� ����������ƽ�е����ʶ��������жϳ�����
����ͼ��ʾ��ȡBB1���е�M������A1M��FM�����ı���A1D1FM��ƽ���ı��Σ������������ε���λ�߶����ɵ�G��B1M���е㣬�����жϳ�����
����A1D1��ƽ��CDD1C1���ɵ�ƽ��A1D1FM��ƽ��CDD1C1�������жϳ�����
��ֱ��D1E��FG�Ľ������ƽ��A1B1C1D1�ϣ�����ƽ��BCC1B1�ϣ������ƽ��A1B1C1D1��ƽ��BCC1B1�Ľ����ϣ������жϳ�����
���ȼ�������̨B1EG-C1D1F�����V1�����ü�����ABGEA1-DCFD1�����Ϊ=${V}_{������A{C}_{1}}$-V1�������жϳ�����
��� �⣺���ڢ٣���ƽ��ABB1A1��ƽ��DCC1D1��ƽ��D1EGF��ƽ��ABB1A1=EG��ƽ��D1EGF��ƽ��DCC1D1=D1F����EG��D1F��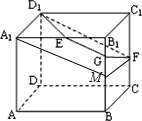
���ڢڣ���ͼ��ʾ��ȡBB1���е�M������A1M��FM�����ı���A1D1FM��ƽ���ı��Σ���A1M��D1F����A1M��EG���ֵ�E��A1B1���е㣬
��G��B1M���е㣬��BG=3GB1��
���ڢۣ���A1D1��ƽ��CDD1C1����ƽ��A1D1FM��ƽ��CDD1C1���ɵ�ƽ��D1EGF��ƽ��CDD1C1�����ܴ�ֱ����˲���ȷ��
���ڢܣ�ֱ��D1E��FG�Ľ������ƽ��A1B1C1D1�ϣ�����ƽ��BCC1B1�ϣ������ƽ��A1B1C1D1��ƽ��BCC1B1�Ľ���B1C1�ϣ���ȷ��
���ڢݣ���${S}_{��F{C}_{1}{D}_{1}}$=$\frac{1}{2}��2��1$=1��${S}_{��{B}_{1}EG}$=$\frac{1}{2}��1��\frac{1}{2}$=$\frac{1}{4}$����B1C1=2��������̨B1EG-C1D1F�����V1=$\frac{1}{3}��2����1+\sqrt{1��\frac{1}{4}}+\frac{1}{4}��$=$\frac{7}{6}$��
�༸����ABGEA1-DCFD1�����Ϊ=${V}_{������A{C}_{1}}$-V1=23-$\frac{7}{6}$=$\frac{41}{6}$�������ȷ��
�ʴ�Ϊ���٢ڢܢݣ�
���� ���⿼���˿ռ���������λ�ù�ϵ�����ж�����������̨��������㹫ʽ�������˿ռ��������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}}{6}$ | B�� | $\frac{2\sqrt{6}}{3}$ | C�� | $\frac{\sqrt{6}}{3}$ | D�� | $\frac{4\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{1}{2}$��1] | B�� | [-1��1] | C�� | [-$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$] | D�� | [-$\frac{\sqrt{3}}{2}$��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{3}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{{\sqrt{3}}}{6}$ | D�� | $\frac{{\sqrt{5}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com