
ЗжЮі ЃЈ1ЃЉЖдвЛЧае§ећЪ§nЖМгаSn=n2+$\frac{1}{2}$anЃЎПЩЕУan+1=Sn+1-SnЃЌЛЏМђећРэМДПЩЕУГіЃЎ
ЃЈ2ЃЉдкSn=n2+$\frac{1}{2}$anжаЃЌСюn=1ЃЌЕУa1=2ЃЌгжa2+a1=6ЃЌНтЕУa2=4ЃЎРћгУЕнЭЦЙиЯЕПЩЕУЃКan+2-an=4ЃЌЪ§Са{an}ЕФЦцЪ§ЯюгыХМЪ§ЯюЗжБ№ЮЊЙЋВюЮЊ4ЕФЕШВюЪ§СаЃЌМДПЩЕУГіЃЎ
ЃЈ3ЃЉfЃЈnЃЉ=ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃМ$\frac{2{a}^{2}-3}{2a\sqrt{2n+1}}$ЖдгквЛЧае§ећЪ§nГЩСЂЃЌЕШМлгк$\sqrt{2n+1}$ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃМ$\frac{2{a}^{2}-3}{2a}$ЖдгквЛЧае§ећЪ§nГЩСЂЃЎСюgЃЈnЃЉ=$\sqrt{2n+1}$ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃЌЭЈЙ§зїЩЬХаЖЯЦфЕЅЕїадМДПЩЕУГіЃЎ
НтД№ ЃЈ1ЃЉжЄУїЃКЁпЖдвЛЧае§ећЪ§nЖМгаSn=n2+$\frac{1}{2}$anЃЎ
Ёрan+1=Sn+1-Sn=$ЃЈn+1ЃЉ^{2}+\frac{1}{2}{a}_{n+1}$-ЃЈn2+$\frac{1}{2}$anЃЉЃЌ
Ёрan+1+an=4n+2ЃЎ
ЃЈ2ЃЉНтЃКдкSn=n2+$\frac{1}{2}$anжаЃЌСюn=1ЃЌЕУa1=2ЃЌ
гжa2+a1=6ЃЌНтЕУa2=4ЃЎ
Ёпan+1+an=4n+2ЃЌan+2+an+1=4n+6ЃЌ
СНЪНЯрМѕЃЌЕУan+2-an=4ЃЌ
ЁрЪ§Са{an}ЕФЦцЪ§ЯюгыХМЪ§ЯюЗжБ№ЮЊЙЋВюЮЊ4ЕФЕШВюЪ§СаЃЌ
ЁрЕБnЮЊХМЪ§ЪБЃЌan=a2+$ЃЈ\frac{n}{2}-1ЃЉ$ЁС4=2nЃЎ
ЕБnЮЊЦцЪ§ЪБЃЌn+1ЮЊХМЪ§ЃЌгЩЩЯЪНМАЃЈ1ЃЉжЊЃКan=4n+2-an+1=2nЃЌ
ЁрЪ§Са{an}ЕФЭЈЯюЙЋЪНЪЧan=2nЃЎ
ЃЈ3ЃЉНтЃКfЃЈnЃЉ=ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃМ$\frac{2{a}^{2}-3}{2a\sqrt{2n+1}}$ЖдгквЛЧае§ећЪ§nГЩСЂЃЌ
ЕШМлгк$\sqrt{2n+1}$ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃМ$\frac{2{a}^{2}-3}{2a}$ЖдгквЛЧае§ећЪ§nГЩСЂЃЎЃЌ
СюgЃЈnЃЉ=$\sqrt{2n+1}$ЃЈ$1-\frac{1}{{a}_{1}}$ЃЉЃЈ$1-\frac{1}{{a}_{2}}$ЃЉЁЃЈ$1-\frac{1}{{a}_{n}}$ЃЉЃЌ
дђгЩЃЈ2ЃЉжЊgЃЈnЃЉЃО0ЃЌ
Ёр$\frac{gЃЈn+1ЃЉ}{gЃЈnЃЉ}$=$\frac{\sqrt{2n+3}ЃЈ1-\frac{1}{{a}_{n+1}}ЃЉ}{\sqrt{2n+1}}$=$\frac{\sqrt{2n+3}ЃЈ1-\frac{1}{2n+2}ЃЉ}{\sqrt{2n+1}}$=$\frac{\sqrt{ЃЈ2n+2ЃЉ^{2}-1}}{2n+2}$ЃМ1ЃЎ
ЁрgЃЈn+1ЃЉЃМgЃЈnЃЉЃЌМДgЃЈnЃЉЕФжЕЫцnЕФдіДѓЖјМѕаЁЃЎ
ЁрnЁЪN*ЪБЃЌgЃЈnЃЉЕФзюДѓжЕЮЊgЃЈ1ЃЉ=$\frac{\sqrt{3}}{2}$ЃЎ
ШєДцдкЪЕЪ§aЃЌЗћКЯЬтвтЃЌдђБига$\frac{2{a}^{2}-3}{2a}$$ЃО\frac{\sqrt{3}}{2}$ЃЌ
МДaЃЈa-$\sqrt{3}$ЃЉ$ЃЈa+\frac{\sqrt{3}}{2}ЃЉ$ЃО0ЃЎ
НтЕУ$-\frac{\sqrt{3}}{2}$ЃМaЃМ0ЃЌЛђa$ЃО\sqrt{3}$ЃЎ
вђДЫЃЌДцдкЪЕЪ§aЃЌЗћКЯЬтвтЃЌЦфШЁжЕЗЖЮЇЮЊ$ЃЈ-\frac{\sqrt{3}}{2}ЃЌ0ЃЉ$ЁШ$ЃЈ\sqrt{3}ЃЌ+ЁоЃЉ$ЃЎ
ЕуЦР БОЬтПМВщСЫЕнЭЦЙиЯЕЁЂЕШВюЪ§СаЕФЭЈЯюЙЋЪНЁЂЁАЗХЫѕЗЈЁБЁЂВЛЕШЪНЕФНтЗЈЁЂЪ§СаЕФЕЅЕїадЃЌПМВщСЫЗжРрЬжТлЗНЗЈЁЂЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ДцдкФГИіЮЛжУЃЌЪЙЕУжБЯпABКЭжБЯпCDДЙжБ | |
| BЃЎ | ДцдкФГИіЮЛжУЃЌЪЙЕУжБЯпACКЭжБЯпBDДЙжБ | |
| CЃЎ | ДцдкФГИіЮЛжУЃЌЪЙЕУжБЯпADКЭжБЯпBCДЙжБ | |
| DЃЎ | ЮоТлЗелЕНЪВУДЮЛжУЃЌвдЩЯШ§зщжБЯпОљВЛДЙжБ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{\sqrt{3}}{2}$ | BЃЎ | $\frac{1}{2}$ | CЃЎ | -$\frac{1}{2}$ | DЃЎ | -$\frac{1}{4}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЕквЛЯѓЯо | BЃЎ | ЕкЖўЯѓЯо | CЃЎ | ЕкШ§ЯѓЯо | DЃЎ | ЕкЫФЯѓЯо |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
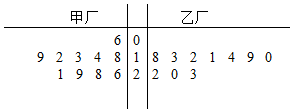 ФГжжВњЦЗЕФжЪСПвдЦфжЪСПжИБъжЕКтСПЃЌжЪСПжИБъжЕдНДѓБэУїжЪСПдНКУЃЌЧвжЪСПжИБъжЕДѓгк17ПЫЪБЃЌИУВњЦЗЮЊгХЕШЦЗЃЎЯждкЮЊСЫНтМзЁЂввСНГЇВњЦЗЕФжЪСПЃЌДгСНГЇЩњВњЕФВњЦЗжаЗжБ№ЫцЛњГщШЁИї10МўбљЦЗЃЌВтСПбљЦЗЕФжЪСПжИБъжЕЃЈЕЅЮЛЃКПЫЃЉ•ШчЭМЪЧВтСПЪ§ОнЕФОЅвЖЭМЃК
ФГжжВњЦЗЕФжЪСПвдЦфжЪСПжИБъжЕКтСПЃЌжЪСПжИБъжЕдНДѓБэУїжЪСПдНКУЃЌЧвжЪСПжИБъжЕДѓгк17ПЫЪБЃЌИУВњЦЗЮЊгХЕШЦЗЃЎЯждкЮЊСЫНтМзЁЂввСНГЇВњЦЗЕФжЪСПЃЌДгСНГЇЩњВњЕФВњЦЗжаЗжБ№ЫцЛњГщШЁИї10МўбљЦЗЃЌВтСПбљЦЗЕФжЪСПжИБъжЕЃЈЕЅЮЛЃКПЫЃЉ•ШчЭМЪЧВтСПЪ§ОнЕФОЅвЖЭМЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com