
| A. | (-2,3) | B. | (-6,0) | C. | [-2,3] | D. | [-6,0] |
分析 先求导,分别求出导函数的最值,再根据不存在x1,x2∈R,使得f′(x1)=g′(x2),得到关于a的不等式解得即可.
解答 解:∵函数f(x)=ex-2ax,函数g(x)=-x3-ax2,
∴f′(x)=ex-2a>-2a,g′(x)=-3x2-2ax=-3(x+$\frac{a}{3}$)2+$\frac{{a}^{2}}{3}$≤$\frac{{a}^{2}}{3}$,
∵不存在x1,x2∈R,使得f′(x1)=g′(x2),
∴-2a≥$\frac{{a}^{2}}{3}$,
解得-6≤a≤0,
故选:D.
点评 本题考查了导数的运算法则和函数的最值问题,以及不等式的解法,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
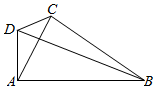 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
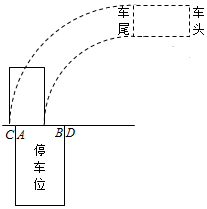 某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com