
分析 (1)求出f(x)的导数,可得切线的斜率和切点,即可得到所求切线的方程;
(2)求出f(x)的导数,求得单调区间,可得最大值-1,即有|f(x)|的最小值;求得g(x)=$\frac{lnx}{x}$的导数,求出最大值,即可得证;
(3)将两数作差可得$\frac{1}{m-n}$[ln$\frac{m}{n}$-$\frac{(\frac{m}{n})^{2}-\frac{m}{n}}{(\frac{m}{n})^{2}+1}$],设t=$\frac{m}{n}$(t>1),即有h(t)=lnt-$\frac{{t}^{2}-t}{{t}^{2}+1}$,求出导数,判断符号,可得单调性,即可得到大小关系.
解答 解:(1)函数f(x)=lnx-x的导数为f′(x)=$\frac{1}{x}$-1,
可得函数f(x)的图象在x=1处的切线斜率为k=0,
切点为(1,-1),
可得切线的方程为y=-1;
(2)证明:f(x)的导数为f′(x)=$\frac{1}{x}$-1,
由f(x)在x>1递减,在0<x<1递增,可得
f(x)在x=1处取得极大值,且为最大值-1,
即有|f(x)|≥1;
又g(x)=$\frac{lnx}{x}$,导数g′(x)=$\frac{1-lnx}{{x}^{2}}$
由g(x)在x>e递减,在0<x<e时递增,
可得g(x)在x=e处取得极大值,且为最大值$\frac{1}{e}$,
则|f(x)|>$\frac{lnx}{x}$成立;
(3)$\frac{f(m)+m-[f(n)+n]}{m-n}$=$\frac{lnm-lnn}{m-n}$,
可得$\frac{f(m)+m-[f(n)+n]}{m-n}$-$\frac{m}{{m}^{2}+{n}^{2}}$
=$\frac{1}{m-n}$[(lnm-lnn)-$\frac{{m}^{2}-mn}{{m}^{2}+{n}^{2}}$]
=$\frac{1}{m-n}$[ln$\frac{m}{n}$-$\frac{(\frac{m}{n})^{2}-\frac{m}{n}}{(\frac{m}{n})^{2}+1}$],
设t=$\frac{m}{n}$(t>1),即有h(t)=lnt-$\frac{{t}^{2}-t}{{t}^{2}+1}$,
h′(t)=$\frac{1}{t}$-$\frac{{t}^{2}+2t-1}{(1+{t}^{2})^{2}}$=$\frac{{t}^{3}(t-1)+t+1}{t(1+{t}^{2})^{2}}$>0,
则h(t)在t>1递增,可得h(t)>h(1)=0,
即有$\frac{f(m)+m-[f(n)+n]}{m-n}$-$\frac{m}{{m}^{2}+{n}^{2}}$>0,
即$\frac{f(m)+m-[f(n)+n]}{m-n}$>$\frac{m}{{m}^{2}+{n}^{2}}$.
点评 本题看出导数的运用:求切线的方程和单调区间、极值和最值,考查不等式的证明,注意运用转化思想,求得最值,考查两数大小比较,注意运用构造函数,运用单调性,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x|x-1|
已知函数f(x)=x|x-1|查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
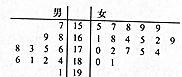 某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com