练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知向量
    a
    与
    b
    的夹角是120°，|
    a
    |=3，|
    a
    +
    b
    |=
    		13
    ，则|
    b
    |=
     
    ．
    考点：平面向量数量积的运算
    专题：计算题,平面向量及应用
    分析：运用向量的平方即为模的平方，以及向量的数量积的定义，解方程即可得到．
    解答： 解：向量
    a
    与
    b
    的夹角是120°，|
    a
    |=3，|
    a
    +
    b
    |=
    		13
    ，
    则（
    a
    +
    b
    ）2=13，
    即有
    a
    2    +
    b
    2    +2
    a
    •
    b
    =13，
    即9+|
    b
    |2+2×3|
    b
    |•cos120°=13，
    即|
    b
    |2-3|
    b
    |-4=0，
    即有|
    b
    |=4（-1舍去），
    故答案为：4．
    点评：本题考查向量的数量积的定义和性质，主要考查向量的平方即为模的平方，考查运算能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在极坐标系中，已知点A（
    		2
    ，0）到直线l：ρsin（θ-
    π
    4
    ）=m（m＞0）的距离为3．
    （1）求实数m值；
    （2）设P是直线l上的动点，Q在线段OP上，且满足|OP||OQ|=1，求点Q轨迹方程，并指出轨迹是什么图形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinα-cosα=-
    		5
    5
    ，180°＜α＜270°，求tanα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若集合A={x|x∈R|ax2+ax+1=0}有两个元素，则a的范围
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某学习小组共9人，在如图所示的方格中选择一个座位，根据以往的学习经验，学习互助伙伴越多，学习成绩越好（互助伙伴指两个学生座位是前后或左右关系且相邻），每个学生期末成
    绩X与互助伙伴数n之间的关系如下表所示：
    n234
    X859095
    （1）完成下表，并求出该小组期末考试成绩的平均值；
    X859095
    频数
    （2）若规定当期末成绩X≥90考核为优秀组员，现从优秀组员中任意选取2人，则这2人不是互助伙伴的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    利用柯西不等式证明平方平均不等式．
    设a1、a2、…，an∈R+，则
    a1+a2+…+an
    n
    ≤
    a12+a22+…+an2
    n
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，PA=PD=AD=2．
    （1）求证：AD⊥平面PQB；
    （2）若PM=
    1
    3
    PC，平面PAD⊥平面ABCD，求二面角M-BQ-C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

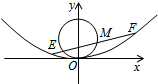    已知抛物线C：x2=2py（p＞0），直线l：y=x+1与抛物线C交于A，B两点，设直线OA，OB的斜率分别为k1．k2（其中O为坐标原点），且k1•k2=-
    1
    4
    ．
    （1）求p的值；
    （2）如图，已知点M（x0，y0）为圆：x2+y2-y=0上异于O点的动点，过点M的直线m交抛物线C于E，F两点．若M为线段EF的中点，求|EF|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设非零向量向量
    OA
    =
    a
    ，
    OB
    =
    b
    ，已知|
    a
    |=2|
    b
    |，（
    a
    +
    b
    ）⊥
    b
    ．
    （1）求
    a
    与
    b
    的夹角；
    （2）在如图所示的直角坐标系xOy中，设B（1，0），已知
    M（
    1
    2
    ，
    5
    		3
    6
    ），
    OM
    =λ1
    a
    +λ2
    b
    （λ1，λ2∈R），求λ1+λ2的值．

    查看答案和解析>>

    同步练习册答案