
���� ��1����M��B1��B2��B3���жԿ�����ʤ���¼��ֱ�ΪA��B��C��M���ٻ�ʤ�������¼�ΪD����$P��A��=\frac{3}{4}$��$P��B��=\frac{2}{3}$��$P��C��=\frac{1}{2}$�������¼�A��B��C��������ɵ�$P��D��=P��ABC��+P��AB\overline C��+P��A\overline BC��+P��\overline ABC��$���Ƚϼ��ɵó���
��2��M��ʤ����X�Ŀ���ȡֵΪ0��1��2��3������������뻥���¼��ĸ��ʼ��㹫ʽ���ɵó���
��� �⣺��1����M��B1��B2��B3���жԿ�����ʤ���¼��ֱ�ΪA��B��C��M���ٻ�ʤ�������¼�ΪD��
��$P��A��=\frac{3}{4}$��$P��B��=\frac{2}{3}$��$P��C��=\frac{1}{2}$��
�����¼�A��B��C�������
��$P��D��=P��ABC��+P��AB\overline C��+P��A\overline BC��+P��\overline ABC��$=$\frac{3}{4}��\frac{2}{3}��\frac{1}{2}+\frac{3}{4}��\frac{2}{3}����1-\frac{1}{2}��+\frac{3}{4}����1-\frac{2}{3}����\frac{1}{2}+��1-\frac{3}{4}����\frac{2}{3}��\frac{1}{2}=\frac{17}{24}$��
����$\frac{17}{24}��\frac{7}{10}$����M����ѡ���յĴ�������
��2��M��ʤ����X�Ŀ���ȡֵΪ0��1��2��3��
��$P��X=0��=P��\overline A\overline B\overline C��=��1-\frac{3}{4}������1-\frac{2}{3}������1-\frac{1}{2}��=\frac{1}{24}$��$P��X=1��=P��A\overline B\overline C��+P��\overline A\overline BC��+P��\overline AB\overline C��=\frac{3}{4}����1-\frac{2}{3}������1-\frac{1}{2}��+��1-\frac{3}{4}������1-\frac{2}{3}����\frac{1}{2}+��1-\frac{3}{4}����\frac{2}{3}����1-\frac{1}{2}��=\frac{6}{24}$$P��X=2��=P��AB\overline C��+P��A\overline BC��+P��\overline ABC��=\frac{3}{4}��\frac{2}{3}����1-\frac{1}{2}��+\frac{3}{4}����1-\frac{2}{3}����\frac{1}{2}+��1-\frac{3}{4}����\frac{2}{3}��\frac{1}{2}=\frac{11}{24}$��
$P��X=3��=P��ABC��=\frac{3}{4}��\frac{2}{3}��\frac{1}{2}=\frac{6}{24}$��
����M��ʤ����X�ķֲ���Ϊ��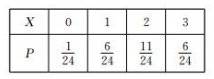
��ѧ����Ϊ$E��X��=0��\frac{1}{24}+1��\frac{6}{24}+2��\frac{11}{24}+3��\frac{6}{24}=\frac{23}{12}$��
���� ���⿼����������뻥���¼��ĸ��ʼ��㹫ʽ�������������ѧ������������������������������������е��⣮


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��3] | B�� | [-1��0�� | C�� | [-1��3] | D�� | ��3��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��b��c��d����ac��bd | |
| B�� | ��ac2��bc2����a��b | |
| C�� | ��a��b��c��d����a-c��b-d | |
| D�� | ��0��a��b������A={x|x=$\frac{1}{a}$}��B={x|x=$\frac{1}{b}$}����A?B |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{2}{3}��$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2}{3}��$ | D�� | $-\frac{2}{3}��$��$\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��e] | B�� | ��1+$\frac{1}{e}$��e] | C�� | ��2��e] | D�� | ��2+$\frac{1}{e}$��e] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
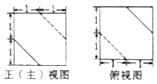 ��֪һ���������ȡ����ȫ�ȵ�С��������õ��ļ����������ͼ����ͼ��ͼ����ü����������ͼΪ��������
��֪һ���������ȡ����ȫ�ȵ�С��������õ��ļ����������ͼ����ͼ��ͼ����ü����������ͼΪ��������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4i | B�� | 4 | C�� | -4i | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{3}$ | B�� | -$\frac{1}{3}$ | C�� | $\frac{1}{3}$ | D�� | $��\frac{2\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com