练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    利用校园内围墙一角和篱笆围成一个面积为128m2的直角梯形花园，已知两围墙所成角为135°（如图），则所用篱笆总长度的最小值为（　　）
    A、16
    		3
    m
    B、32m
    C、64m
    D、16m
    考点：基本不等式在最值问题中的应用
    专题：计算题,不等式的解法及应用
    分析：先设出BD=x，篱笆长度为y，进而分别表示出CD，AB，进而根据梯形面积公式建立等式，表示出y，利用基本不等式求得y的最小值．
    解答： 解：如图，设BD=x，设篱笆长度为y，则CD=y-x，AB=y-2x，
    梯形的面积为
    (y-2x+y-x)•x
    2
    =128，
    整理得y=
    128
    x
    +
    3x
    2
    ≥16
    		3
    ，当
    128
    x
    =
    3
    2
    x等号成立，
    所以篱笆总长度最小为16
    		3
    m．
    故选：A．
    点评：本题主要考查了基本不等式的应用．解题的关键是根据题意建立数学模型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列选项中不是右图中几何体的三种视图之一的是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若△ABC的三边长分别为5，5，6，设最大内角为α，则tanα=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

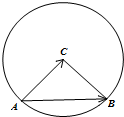    如图，定圆C半径为r，A为圆C上的一个定点，B为圆C上的动点，若点A，B，C不共线，且|
    AB
    -t
    AC
    |≥|
    BC
    |    对任意t∈（0，+∞）恒成立，则
    AB
    •
    AC
    =
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知{an}是由正数组成的数列，其前n项和Sn与an之间满足：an+
    1
    2
    =
    		2Sn+
    1
    4
    （n≥1且n∈N*）．
    （Ⅰ）求数列{an}的通项an；
    （Ⅱ）设bn=（
    1
    2
    ）nan，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设变量x，y满足
    x-y≤2
    0≤x+y≤4
    0≤y≤3
    ，则z=3x+2y的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    质点沿直线运动的路程与时间的关系是S=
    5t
    ，则质点在t=32时的速度为？（请用导数相关知识解答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    点（x，y）的坐标x，y都是有理数时，该点称为有理点，在半径为r，圆心为（a，b）的圆中，若a∈Q，b∈Q，则这个圆上的有理点的数目为（　　）
    A、最多有一个
    B、最多有两个
    C、最多有三个
    D、可以有无穷多个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

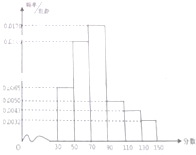    某县为“中学生知识竞赛”进行选取性测试，规定：成绩大于或等于90分的右参赛资格，90分以下（不包括90分）的则被淘汰，若现有1000人参加测试，学生成绩的频率分别直方图如图：
    （1）根据频率分别直方图，求获得参赛资格的人数并估算这1000名学生测试的平均值
    （2）若知识竞赛分初赛和复赛，在初赛中每人最多有5道选题答题的机会，累计大队3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
    1
    9
    ，求甲在初赛中答题个数的分布列及数学期望．

    查看答案和解析>>

    同步练习册答案