考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)f′(x)=(ax
2-x-a+1)e
x=(ax+a-1)(x-1)e
x,对a分类讨论:当a=0时,f′(x)=-(x-1)e
x,即可得出单调性;当a>0时,f′(x)=a
(x-)(x-1)e
x,令
=1,解得a=
.当a=
时,当
0<a<时,当a
>时,比较
与1的大小关系即可得出单调性;
(2)当a=1时,函数f(x)在(0,1)上单调递减;在(1,2)上单调递增.对任意x
1∈(0,2),都有f(x
1)≥f(1)=e.又对任意x
1∈(0,2),存在x
2∈(1,2),使f(x
1)≥g(x
2),e≥g(x
2),即x
2∈(1,2)时有解,g(x
2)=
,即存在x
2∈(1,2),使得
b≤.令h(x)=
,利用导数研究其单调性极值与最值即可得出.
解答:
解:(1)f′(x)=(ax
2-x-a+1)e
x=(ax+a-1)(x-1)e
x,
a=0时,f′(x)=-(x-1)e
x,
∴当x>1时,f′(x)<0,函数f(x)单调递减;当x<1时,f′(x)>0,函数f(x)单调递增.
当a>0时,f′(x)=a
(x-)(x-1)e
x,
令
=1,解得a=
.
当a=
时,
f′(x)=(x-1)2ex≥0,函数f(x)在R上单调递增;
当
0<a<时,
>1,x∈(-∞,1)时,f′(x)>0,函数f(x)单调递增;
x∈(1,),f′(x)<0,函数f(x)单调递减;
x∈(,+∞),f′(x)>0,函数f(x)单调递增.
当a
>时,
<1,x∈(-∞,
)时,f′(x)>0,函数f(x)单调递增;
x∈(,1),f′(x)<0,函数f(x)单调递减;x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增.
综上可得:当a=0时,当x>1时,函数f(x)单调递减;当x<1时,函数f(x)单调递增.
当a=
时,函数f(x)在R上单调递增;
当
0<a<时,x∈(-∞,1)时,函数f(x)单调递增;
x∈(1,),函数f(x)单调递减;
x∈(,+∞),函数f(x)单调递增.
当a
>时,x∈(-∞,
)时,函数f(x)单调递增;
x∈(,1),函数f(x)单调递减;x∈(1,+∞)时,函数f(x)单调递增.
(2)当a=1时,函数f(x)在(0,1)上单调递减;在(1,2)上单调递增.
对任意x
1∈(0,2),都有f(x
1)≥f(1)=e.
又对任意x
1∈(0,2),存在x
2∈(1,2),使f(x
1)≥g(x
2),
∴e≥g(x
2),即x
2∈(1,2)时有解,
g(x
2)=
,∴存在x
2∈(1,2),使得
≤e,即存在x
2∈(1,2),使得
b≤.
令h(x)=
,x∈(1,2),h′(x)=
,
令h′(x)=0,解得x=
,
当x∈
(1,)时,h′(x)>0,函数h(x)单调递增;当x∈
(,2)时,h′(x)<0,函数h(x)单调递减.
∴当x=
时,h(x)的最大值为
h()=
,
综上可得:实数b的取值范围是
(-∞,].
点评:本题考查了利用导数研究其单调性极值与最值,考查了分类讨论思想方法,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案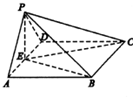 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是等边三角形,平面PAD⊥平面ABCD,E是线段AD的中点.