
| A. | [$\frac{1}{3}$,$\frac{1}{2}$) | B. | [$\frac{2}{5}$,$\frac{1}{2}$) | C. | [$\frac{2}{5}$,1) | D. | (0,$\frac{1}{2}$) |
分析 由分段函数的性质结合一次函数和对数函数的单调性,列出不等式组,由此能求出实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{(2a-1)x+a(x<2)}\\{lo{g}_{a}(x-1)(x≥2)}\end{array}\right.$是R上的减函数,
∴$\left\{\begin{array}{l}{2a-1<0}\\{0<a<1}\\{lo{g}_{a}(2-1)≤2(2a-1)+a}\end{array}\right.$,
解得$\frac{2}{5}≤a<\frac{1}{2}$.
∴实数a的取值范围是[$\frac{2}{5}$,$\frac{1}{2}$).
故选:B.
点评 本题考查满足条件的实数的取值范围的求法,是中档题,解题时要认真审题,注意分段函数的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥n,则n∥α | D. | m⊥α,m∥n,则n⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或11 | B. | 1 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
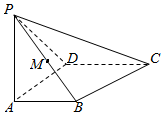 四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.
四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
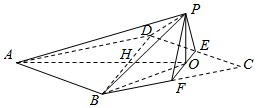 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4}^{n}-1}{3}$ | B. | $\frac{({2}^{n}-1)^{2}}{3}$ | C. | 4n-1 | D. | (2n-1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com