
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 4500 |
| 15000 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
| 300×(45×60-165×30)2 |
| 210×90×75×225 |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
| 4n |
| anan+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| ln2 |
| an |
| bn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
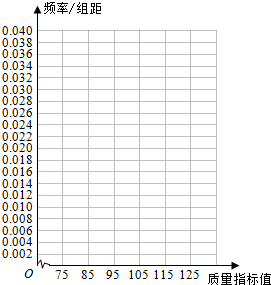
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com