
分析 (1)由三角形面积可得$\frac{1}{2}bc•sinA=3$,由0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,得0≤bccosA≤6,两式联立可得tanA≥1,从而求得A的范围;
(2)把A代入f(θ)=2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ,降幂后利用辅助角公式化简,由A的范围求得f(A)的值域.
解答 解:(1)∵S△ABC=3,
∴$\frac{1}{2}bc•sinA=3$,即bcsinA=6,则bc=$\frac{6}{sinA}$,①
∵0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,
∴0≤bccosA≤6,②
把①代入②得:$0≤\frac{cosA}{sinA}≤1$,即tanA≥1,
∴A∈[$\frac{π}{4},\frac{π}{2}$).
当A=$\frac{π}{2}$时,①化为bc=6,此时②成立.
∴A∈[$\frac{π}{4},\frac{π}{2}$];
(2)f(A)=2sin2($\frac{π}{4}$+A)-$\sqrt{3}$cos2A=$1-cos(\frac{π}{2}+2A)-\sqrt{3}cos2A$
=1+sin2A-$\sqrt{3}$cos2A=1+2sin(2A-$\frac{π}{3}$).
∵A∈[$\frac{π}{4},\frac{π}{2}$],∴$2A-\frac{π}{3}$∈[$\frac{π}{6},\frac{2π}{3}$],
∴sin(2A-$\frac{π}{3}$)∈[$\frac{1}{2}$,1].
∴f(A)∈[2,3].
点评 本题考查平面向量的数量积运算,考查三角函数的化简求值,是中档题.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 42种 | B. | 72种 | C. | 84种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
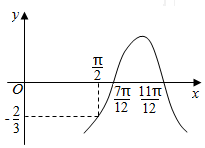
| A. | 函数f(x)的最小周期为$\frac{2π}{3}$ | |
| B. | 图象f(x)的图象可由g(x)=Acos(ωx)的图象向右平移$\frac{π}{12}$个单位得到 | |
| C. | 函数f(x)的图象关于直线x=$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间($\frac{π}{4}$,$\frac{π}{2}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+d}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com