练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．设复数z满足iz=1+2i，则z的共轭复数的虚部为（　　）
    A．iB．-iC．-1D．1

    分析 利用复数的运算法则、共轭复数的定义、虚部的定义即可得出．

    解答 解：iz=1+2i，∴-i•iz=-i（1+2i），z=-i+2
    则z的共轭复数$\overline{z}$=2+i的虚部为1．
    故选：D．

    点评 本题考查了复数的运算法则、共轭复数的定义、虚部的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+2$\overrightarrow{b}$|，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为-$\frac{1}{4}$，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$等于（　　）
    A．$\frac{1}{2}$B．$\frac{2}{3}$C．$\frac{3}{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题：今有望海岛，立两表齐，高三丈，前後相去千步，令後表与前表相直．从前表却行一百二十三步，人目著地取望岛峰，与表末参合．从後表却行百二十七步，人目著地取望岛峰，亦与表末参合．问岛高几何？译文如下：要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，前后两杆相距BD=1000步，使后标杆杆脚D与前标杆杆脚B与山峰脚H在同一直线上，从前标杆杆脚B退行123步到F，人眼著地观测到岛峰，A、C、F三点共线，从后标杆杆脚D退行127步到G，人眼著地观测到岛峰，A、E、G三点也共线，则山峰的高度AH=（　　） 步（古制：1步=6尺，1里=180丈=1800尺=300步）
    A．1250B．1255C．1230D．1200

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若实数a满足x+lgx=2，实数b满足x+10x=2，函数f（x）=$\left\{\begin{array}{l}{2ln（x+2）-\frac{a+b}{2}，x≤0}\\{{x}^{2}-2，x＞0}\end{array}\right.$，则关于x的方程f（x）=x解的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

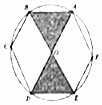    10．已知正六边形ABCDEF内接于圆O，连接AD，BE，现在往圆O内投掷2000粒小米，则可以估计落在阴影区域内的小米的粒数大致是（　　）（参考数据：$\frac{π}{\sqrt{3}}$=1.82，$\frac{\sqrt{3}}{π}$=0.55）
    A．550B．600C．650D．700

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知P是圆x2+y2=R2上的一个动点，过点P作曲线C的两条互相垂直的切线，切点分别为M，N，MN的中点为E．若曲线C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），且R2=a2+b2，则点E的轨迹方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{a^2}+{b^2}}}}$．若曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞b＞0）$，且R2=a2-b2，则点E的轨迹方程是（　　）
    A．$\frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{a^2}+{b^2}}}}$B．$\frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{a^2}-{b^2}}}}$
    C．$\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{a^2}+{b^2}}}}$D．$\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{{a^2}-{b^2}}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知数列{an}满足，${a_n}=2+2{cos^2}\frac{nπ}{2}$，n∈N*，等差数列{bn}满足a1=2b1，a2=b2．
    （1）求bn；
    （2）记cn=a2n-1b2n-1+a2nb2n，求cn；
    （3）求数列{anbn}前2n项的和S2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=|x-a|（a∈R）．
    （1）若a=1，解不等式f（x）＞$\frac{1}{2}$（x+1）；
    （2）若不等式f（x）+|x-2|≤3有解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在平面直角坐标系xOy中，已知直线$\left\{\begin{array}{l}{x=-\frac{3}{2}+\frac{\sqrt{2}}{2}l}\\{y=\frac{\sqrt{2}}{2}l}\end{array}\right.$（l为参数）与曲线$\left\{\begin{array}{l}{x=\frac{1}{8}{t}^{2}}\\{y=t}\end{array}\right.$（t为参数）相交于A，B两点，求线段AB的长．

    查看答案和解析>>

    同步练习册答案