
分析 由分母不为零求出函数的定义域,根据指数函数的性质、反比例函数的性质求出函数的值域.
解答 解:由2x-1≠0得x≠0,∴函数的定义域为{x|x≠0},
∵2x>0,∴2x-1>-1且2x-1≠0,
则$\frac{1}{{2}^{x}-1}<-1$或$\frac{1}{{2}^{x}-1}>0$,
∴$\frac{1}{2}+\frac{1}{{2}^{x}-1}<-\frac{1}{2}$或$\frac{1}{2}+\frac{1}{{2}^{x}-1}>\frac{1}{2}$,
∴函数的值域是$(-∞,-\frac{1}{2})∪(\frac{1}{2},+∞)$.
点评 本题考查函数的定义域和值域的求解,利用指数函数的性质是解决本题的关键.


科目:高中数学 来源: 题型:解答题
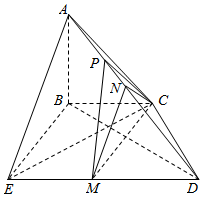 如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.
如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
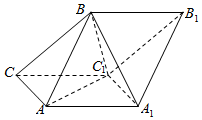 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )
如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )| A. | $\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 3$\sqrt{3}$π | D. | $\frac{3\sqrt{3}π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
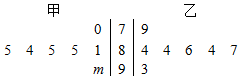
| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | D. | $\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$的大小不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com