练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．若1+2+4+…+2n-1=127，求自然数n．

    分析 根据等比数列的前n项和公式可求得2n-1=127，从而解得．

    解答 解：由等比数列性质可知，
    1+2+4+…+2n-1
    =$\frac{1（1-{2}^{n}）}{1-2}$
    =2n-1=127，
    故2n=128，
    故n=7．

    点评 本题考查了等比数列的性质的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．$\overrightarrow{a}•\overrightarrow{b}$=6，|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2$\sqrt{2}$，则，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=45°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求下列函数的导数：
    （1）y=（2x2+3x+1）5；
    （2）y=esinx；
    （3）y=tan$\frac{1}{x}$；
    （4）y=$\sqrt{1-{x}^{2}}$；
    （5）y=ln（lnx）；
    （6）y=cos（2x+$\frac{π}{6}$）；
    （7）y=ln$\frac{x-1}{x+1}$；
    （8）y=2xcos3x；
    （9）y=x2lnx．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在区间（0，+∞）上，函数y=lg（1+$\frac{1}{x}$）是（　　）
    A．增函数，且y＞0B．增函数，且y＜0C．减函数，且y＞0D．减函数，且y＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

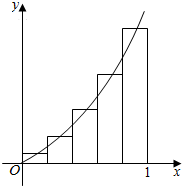    18．求由抛物线f（x）=x2，直线x=1以及x轴所围成的平面图形的面积时，若将区间[0，1]5等分，如图所示，以小区间中点的纵坐标为高，所有小矩形的面积之和为0.33．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知集合A={0，1，3}，B={x|x2-3x=0}，则A∩B={0，3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

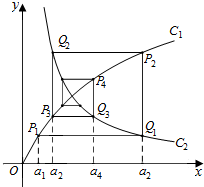    12．如图，已知曲线C1：y=$\frac{2x}{x+1}$（x＞0）及曲线C2：y=$\frac{1}{3x}$（x＞0），C1上的点P1的横坐标为a1（0＜a1＜$\frac{1}{2}$）．从C1上的点Pn（n∈N+）作直线平行于x轴，交曲线C2于点Qn，再从点Qn作直线平行于y轴，交曲线C1于点Pn+1．点Pn（n=1，2，3，…）的横坐标构成数列{an}
    （Ⅰ）试求an+1与an之间的关系，并证明：a2n-1＜$\frac{1}{2}＜{a_{2n}}（n∈{N_+}）$；
    （Ⅱ）若a1=$\frac{1}{3}$，求证：|a2-a1|+|a3-a2|+…+|an+1-an|＜$\frac{4}{3}（n∈{N_+}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．奇函数f（x），当x＜0时，有f（x）=x（2-x），则f（4）的值为（　　）
    A．12B．-12C．-24D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．定义在R上的函数f（x）满足f（x+2）=f（x），当x∈[0，2）时，f（x）=$\left\{\begin{array}{l}{\frac{1}{2}-2{x}^{2}，0≤x＜1}\\{-{2}^{1-|x-\frac{3}{2}|}，1≤x＜2}\end{array}\right.$，函数g（x）=（2x-x2）ex+m，若?x1∈[-4，-2]，?x2∈[-1，2]，使得不等式f（x1）-g（x2）≥0成立，则实数m的取值范围是（　　）
    A．（-∞，-2]B．（-∞，$\frac{3}{e}$+2]C．[$\frac{3}{e}$+2，+∞）D．（-∞，$\frac{3}{e}$-2]

    查看答案和解析>>

    同步练习册答案