
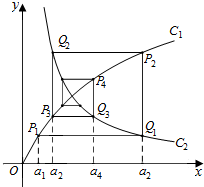
 如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}
如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}分析 (Ⅰ)由已知,Pn$({a}_{n},\frac{2{a}_{n}}{{a}_{n}+1})$,从而有${Q_n}({a_{n+1}},\frac{{2{a_n}}}{{{a_n}+1}})$,由Qn在y=$\frac{1}{3x}$上,代入可得 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,由a1>0,及 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,知an>0,下证:${a_{2n-1}}<\frac{1}{2}<{a_{2n}}$
解法一:由${a}_{n+1}-\frac{1}{2}$=$\frac{-2({a}_{n}-\frac{1}{2})}{6{a}_{n}}$,可得an+1$-\frac{1}{2}$与${a}_{n}-\frac{1}{2}$异号,即可证明.
解法二:由 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,可得${a}_{n+1}-\frac{1}{2}$=$\frac{-2({a}_{n}-\frac{1}{2})}{6{a}_{n}}$,${a}_{n+1}+\frac{1}{3}$=$\frac{3({a}_{n}+\frac{1}{3})}{6{a}_{n}}$,可得$\frac{{{a_{n+1}}-\frac{1}{2}}}{{{a_{n+1}}+\frac{1}{3}}}=-\frac{2}{3}•\frac{{{a_n}-\frac{1}{2}}}{{{a_n}+\frac{1}{3}}}$,利用等比数列的通项公式可得an,进而证明.
(Ⅱ)由a2n+1=$\frac{{a}_{2n}+1}{6{a}_{2n}}$=$\frac{\frac{{a}_{2n-1}+1}{6{a}_{2n-1}}+1}{6\frac{{a}_{2n-1}+1}{6{a}_{2n-1}}}$=$\frac{7{a}_{2n-1}+1}{6({a}_{2n-1}+1)}$,可得a2n+1-a2n-1=$\frac{7{a}_{2n-1}+1}{6({a}_{2n-1}+1)}$-a2n-1=$\frac{-2({a}_{2n}-\frac{1}{2})(3{a}_{2n-1}+1)}{6({a}_{2n-1}+1)}$,由$0<{a_{2n-1}}<\frac{1}{2}$,可得a2n+1>a2n-1,可得${a}_{2n}>\frac{1}{2}$>a2n-1>a2n-3>…>a1.可知an≥a1,因此|an+2-an+1|=$\frac{|{a}_{n+1}-{a}_{n}|}{6{a}_{n}{a}_{n+1}}$=$\frac{|{a}_{n+1}-{a}_{n}|}{{a}_{n}+1}$$≤\frac{{|{a_{n+1}}-{a_n}|}}{{{a_1}+1}}$=$\frac{3}{4}|{a_{n+1}}-{a_n}|$,利用递推关系及其等比数列的前n项和公式即可证明.
解答 解:(Ⅰ)由已知,Pn$({a}_{n},\frac{2{a}_{n}}{{a}_{n}+1})$,从而有${Q_n}({a_{n+1}},\frac{{2{a_n}}}{{{a_n}+1}})$,
因为Qn在y=$\frac{1}{3x}$上,所以有$\frac{2{a}_{n}}{{a}_{n}+1}$=$\frac{1}{3{a}_{n+1}}$,
解得 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,…(3分)
由a1>0,及 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,知an>0,
下证:${a_{2n-1}}<\frac{1}{2}<{a_{2n}}$
解法一:因为${a}_{n+1}-\frac{1}{2}$=$\frac{-2({a}_{n}-\frac{1}{2})}{6{a}_{n}}$,所以an+1$-\frac{1}{2}$与${a}_{n}-\frac{1}{2}$异号,
注意到${a}_{1}-\frac{1}{2}$<0,知${a}_{2n-1}-\frac{1}{2}$<0,${a}_{2n}-\frac{1}{2}$>0,
即${a_{2n-1}}<\frac{1}{2}<{a_{2n}}$…(8分)
解法二:由 ${a}_{n+1}=\frac{{a}_{n}+1}{6{a}_{n}}$,可得${a}_{n+1}-\frac{1}{2}$=$\frac{-2({a}_{n}-\frac{1}{2})}{6{a}_{n}}$,${a}_{n+1}+\frac{1}{3}$=$\frac{3({a}_{n}+\frac{1}{3})}{6{a}_{n}}$,
所以有$\frac{{{a_{n+1}}-\frac{1}{2}}}{{{a_{n+1}}+\frac{1}{3}}}=-\frac{2}{3}•\frac{{{a_n}-\frac{1}{2}}}{{{a_n}+\frac{1}{3}}}$,即$\left\{{\frac{{{a_n}-\frac{1}{2}}}{{{a_n}+\frac{1}{3}}}}\right\}$是以$-\frac{2}{3}$为公比的等比数列;
设$t=\frac{{{a_1}-\frac{1}{2}}}{{{a_1}+\frac{1}{3}}}$,则$\frac{{{a_n}-\frac{1}{2}}}{{{a_n}+\frac{1}{3}}}=t•{(-\frac{2}{3})^{n-1}}$
解得${a_n}=\frac{{\frac{1}{2}+\frac{t}{3}•{{(-\frac{2}{3})}^{n-1}}}}{{1-t•{{(-\frac{2}{3})}^{n-1}}}}$,…(6分)
从而有${a_n}-\frac{1}{2}=\frac{{\frac{1}{2}+\frac{t}{3}•{{(-\frac{2}{3})}^{n-1}}}}{{1-t•{{(-\frac{2}{3})}^{n-1}}}}=\frac{{\frac{5}{6}t}}{{{{(-\frac{3}{2})}^{n-1}}-t}}$
由$0<{a_1}<\frac{1}{2}$可得$-\frac{3}{2}<t<0$,
所以${a_{2n-1}}-\frac{1}{2}=\frac{{\frac{5}{6}t}}{{{{(\frac{9}{4})}^{n-1}}-t}}<0$,${a_{2n}}-\frac{1}{2}=\frac{{\frac{5}{6}t}}{{-{{(\frac{3}{2})}^{2n-1}}-t}}>0$.
所以${a_{2n-1}}<\frac{1}{2}<{a_{2n}}$.…(8分)
(Ⅱ)证明:因为a2n+1=$\frac{{a}_{2n}+1}{6{a}_{2n}}$=$\frac{\frac{{a}_{2n-1}+1}{6{a}_{2n-1}}+1}{6\frac{{a}_{2n-1}+1}{6{a}_{2n-1}}}$=$\frac{7{a}_{2n-1}+1}{6({a}_{2n-1}+1)}$,
所以a2n+1-a2n-1=$\frac{7{a}_{2n-1}+1}{6({a}_{2n-1}+1)}$-a2n-1=$\frac{-2({a}_{2n}-\frac{1}{2})(3{a}_{2n-1}+1)}{6({a}_{2n-1}+1)}$,
因为$0<{a_{2n-1}}<\frac{1}{2}$,所以a2n+1>a2n-1,
所以有${a}_{2n}>\frac{1}{2}$>a2n-1>a2n-3>…>a1.
从而可知an≥a1 …(10分)
故|an+2-an+1|=$|\frac{{a}_{n+1}+1}{6{a}_{n+1}}-\frac{{a}_{n}+1}{6{a}_{n}}|$=$\frac{|{a}_{n+1}-{a}_{n}|}{6{a}_{n}{a}_{n+1}}$=$\frac{|{a}_{n+1}-{a}_{n}|}{{a}_{n}+1}$$≤\frac{{|{a_{n+1}}-{a_n}|}}{{{a_1}+1}}$=$\frac{3}{4}|{a_{n+1}}-{a_n}|$…(12分)
所以$|{a_{n+1}}-{a_n}|≤\frac{3}{4}|{a_n}-{a_{n-1}}|≤{(\frac{3}{4})^2}|{a_{n-1}}-{a_{n-2}}|≤…≤{(\frac{3}{4})^{n-1}}|{a_2}-{a_1}|=\frac{1}{3}•{(\frac{3}{4})^{n-1}}$…(13分)
所以|a2-a1|+|a3-a2|+|a4-a3|+…+|an+1-an|$≤\frac{1}{3}[1+\frac{3}{4}+{(\frac{3}{4})^2}+…+{(\frac{3}{4})^{n-1}}]$=$\frac{1}{3}×\frac{{1-{{(\frac{3}{4})}^n}}}{{1-\frac{3}{4}}}$=$\frac{4}{3}[1-{(\frac{3}{4})^n}]$$<\frac{4}{3}$…(15分)
点评 本题考查了函数关系式、等比数列的通项公式及其前n项和公式、不等式的性质、递推关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 有效 | 无效 | 合计 | |
| 使用方案A组 | 96 | 120 | |
| 使用方案B组 | 72 | ||
| 合计 | 32 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com