
分析 由等比数列的前几项求出通项公式,把-$\frac{32}{81}$代入通项公式求得n值得答案.
解答 解:由等比数列3,-2,$\frac{4}{3}$,-$\frac{8}{9}$,…,可得${a}_{1}=3,q=-\frac{2}{3}$,
则${a}_{n}=3•(-\frac{2}{3})^{n-1}$,
由$3•(-\frac{2}{3})^{n-1}=-\frac{32}{81}$,解得:n=6.
∴-$\frac{32}{81}$是等比数列3,-2,$\frac{4}{3}$,-$\frac{8}{9}$,…的第6项.
点评 本题考查等比数列的通项公式,是基础的计算题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 121对 | B. | 108对 | C. | 21对 | D. | 60对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增函数,且y>0 | B. | 增函数,且y<0 | C. | 减函数,且y>0 | D. | 减函数,且y<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
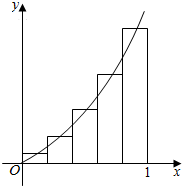 求由抛物线f(x)=x2,直线x=1以及x轴所围成的平面图形的面积时,若将区间[0,1]5等分,如图所示,以小区间中点的纵坐标为高,所有小矩形的面积之和为0.33.
求由抛物线f(x)=x2,直线x=1以及x轴所围成的平面图形的面积时,若将区间[0,1]5等分,如图所示,以小区间中点的纵坐标为高,所有小矩形的面积之和为0.33.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
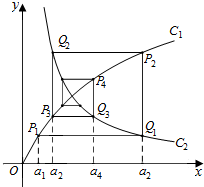 如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}
如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}查看答案和解析>>
科目:高中数学 来源: 题型:解答题
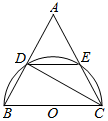 已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.
已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com