
分析 (1)把直线l的方程整理成m(2x+y-7)+(x+y-4)=0,由于m的任意性,有$\left\{\begin{array}{l}2x+y-7=0\\ x+y-4=0\end{array}\right.$,解此方程组,得直线l过定点;
(2)当直线l与DC垂直时,被截得的弦最短,即可得出结论.
解答 (1)证明:把直线l的方程整理成m(2x+y-7)+(x+y-4)=0
由于m的任意性,有$\left\{\begin{array}{l}2x+y-7=0\\ x+y-4=0\end{array}\right.$,解此方程组,得$\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.$,
所以直线l恒过定点D(3,1);
(2)解:当直线l与DC垂直时,被截得的弦最短,
此时,直线l与DC的斜率kl•kCD=-1,
由直线l的方程得${k_l}=-\frac{2m+1}{m+1}$,由点C、D的坐标得${k_{CD}}=\frac{2-1}{1-3}=-\frac{1}{2}$
∴$({-\frac{2m+1}{m+1}})•({-\frac{1}{2}})=-1$,解得$m=-\frac{3}{4}$,
所以,当$m=-\frac{3}{4}$时,直线l被圆C截得的弦最短.
点评 本题考查直线过定点的证明,考查直线与圆的位置关系,正确转化是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{y}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{8}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (0,1) | C. | $({1,\sqrt{2}})$ | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
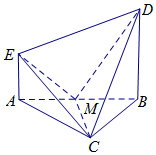 如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.
如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com