【题目】
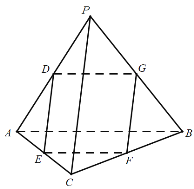
如图，在四面体
中，
点
分别是棱
的中点．
（Ⅰ）求证：
平面
；
（Ⅱ）求证：四边形
为矩形；
（Ⅲ）是否存在点
，到四面体六条棱的中点 的距离相等？说明理由．
【答案】略
【解析】
：证明：（Ⅰ）因为D，E分别为AP，AC的中点，所以DE//PC．又因为DE
平面BCP，所以DE//平面BCP．
（Ⅱ）因为D，E，F，G分别为AP，AC，BC，PB的中点，
所以DE//PC//FG，DG//AB//EF．所以四边形DEFG为平行四边形，
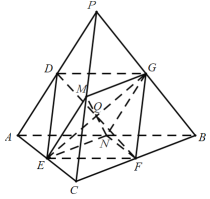
又因为PC⊥AB，所以DE⊥DG，所以四边形DEFG为矩形．
（Ⅲ）存在点Q满足条件，理由如下：连接DF，EG，设Q为EG的中点
由（Ⅱ）知，DF∩EG=Q，且QD=QE=QF=QG=
EG.
分别取PC，AB的中点M，N，连接ME，EN，NG，MG，MN．
与（Ⅱ）同理，可证四边形MENG为矩形，其对角线点为EG的中点Q，
且QM=QN=EG，所以Q为满足条件的点.
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】今年，楼市火爆，特别是一线城市.某一线城市采取“限价房”摇号制度，客户以家庭为单位进行抽签，若有
套房源，则设置个中奖签，客户抽到中奖签视为中签，中签家庭可以在指定小区提供的房源中随机抽取一个房号，现共有20户家庭去抽取6套房源．
（l）求每个家庭能中签的概率；
（2）已知甲、乙两个友好家庭均已中签，并共同前往某指定小区抽取房号，目前该小区剩余房源有某单元27、28两个楼层共6套房，其中，第27层有2套房，第28层有4套房．记甲、乙两个家庭抽取到第28层的房源套数为
，求的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义域为A的函数f(x)，若对任意的x1，x2∈A，都有f(x1＋x2)－f(x1)≤f(x2)，则称函数f(x)为“定义域上的M函数”，给出以下五个函数：
①f(x)＝2x＋3，x∈R；②f(x)＝x2，x∈
；③f(x)＝x2＋1，x∈
；④f(x)＝sin x，x∈
；⑤f(x)＝log2x，x∈[2，＋∞)．
其中是“定义域上的M函数”的有( )
A. 2个 B. 3个
C. 4个 D. 5个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设点
为抛物线
外一点，过点作抛物线
的两条切线
，
，切点分别为
，
．
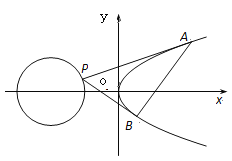
（Ⅰ）若点为
，求直线
的方程；
（Ⅱ）若点为圆
上的点，记两切线，的斜率分别为
，
，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，下列四个命题中真命题的序号是（ ）
(1)
是偶函数；(2)当且仅当
时，有最小值；
(3)在
上是增函数；(4)方程
有无数个实根.
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在数列
中，若
(
，
，
为常数)，则称为“等方差数列”.下列对“等方差数列”的判断：
①若是等方差数列，则
是等差数列；
②
是等方差数列；
③若是等方差数列，则
(
，
为常数)也是等方差数列.其中正确命题序号为
__________(写出所有正确命题的序号).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在
上的函数
，如果满足；对任意
，存在常数
，都有
成立，则称是上的有界函数，其中
称为函数的上界.已知函数
.
（Ⅰ）当
时，求函数在
上的值域，并判断函数在上是否为有界函数，请说明理由；
（Ⅱ）若是
上的有界函数，且的上界为3，求实数
的取值范围；
（Ⅲ）若
，求函数
在
上的上界
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)＝loga(1＋
x)，g(x)＝loga(1－x)，(a>0且a≠1)，若h(x)＝f(x)－g(x)．
(1)求函数h(x)的定义域；
(2)判断h(x)的奇偶性，并说明理由；
(3)若f(2)＝1，求使h(x)>0成立的x的集合．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
