
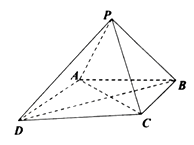
【题目】如图,在四棱锥 ![]() 中,
中, ![]() 、
、 ![]() 、
、 ![]() 均为等边三角形,
均为等边三角形, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】解:(Ⅰ)因为 ![]() ,
, ![]() ,
, ![]() 为公共边,
为公共边,
所以 ![]() ,
,
所以 ![]() ,又
,又 ![]() ,
,
所以 ![]() ,且
,且 ![]() 为
为 ![]() 中点.
中点.
又 ![]() ,所以
,所以 ![]() ,
,
又 ![]() ,所以
,所以 ![]() ,结合
,结合 ![]() ,
,
可得 ![]() ,
,
所以 ![]() ,
,
即 ![]() ,又
,又 ![]() ,
,
故 ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() ,所以
,所以 ![]() .
.
又 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
(Ⅱ)以 ![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 ![]() 如图所示,
如图所示,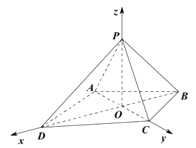
不妨设 ![]() ,易得
,易得 ![]() ,
, ![]() ,
,
则 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
设平面 ![]() 的法向量为
的法向量为 ![]() ,则
,则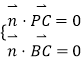 ,即
,即 ![]() ,解得
,解得 ![]() ,
,
令 ![]() 得
得 ![]() ,
,
设直线 ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() ,则
,则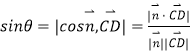
![]() ,
,
所以 ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 ![]()
【解析】(Ⅰ)根据题目中所给的条件的特点,由△ABD和△CBD相似,可得∠ABD=∠CBD,AC⊥BD,即可得PO⊥AC,即PO⊥OB,又PO⊥BD.最后利用线面垂直的判定即可证得结论.
(Ⅱ)根据题意,以O为原点,建立空间直角坐标系O-xyz,求出平面PBC的法向量,利用向量夹角公式求解即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( ) 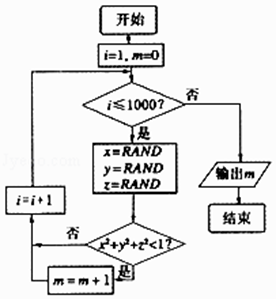
A.3.119
B.3.126
C.3.132
D.3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.
(Ⅰ) 若BC1∥平面A1CD,确定D的位置,并说明理由;
(Ⅱ) 在(Ⅰ)的条件下,求二面角A1D﹣C﹣BC1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|.
(Ⅰ) 解不等式f(x+8)≥10﹣f(x);
(Ⅱ) 若|x|>1,|y|<1,求证:f(y)<|x|f( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和为Sn , 且Sn满足n(n+1)Sn2+(n2+n﹣1)Sn﹣1=0(n∈N*),则S1+S2+…+S2017= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com