
分析 分析题目中的要求,发现这是一个累加型的问题,故可能用循环结构来实现,在编写算法的过程中要注意,累加的初始值为1,累加值每一次增加1,退出循环的条件是累加结果>500,即可得到流程图,进而可得程序.
解答 解:由于1+3+5+…+n=n+n(n-1)=n2>500,可得:n>22.4,
可得:满足1+3+5+…+n>500的最小自然数n为23.
程序框图如下: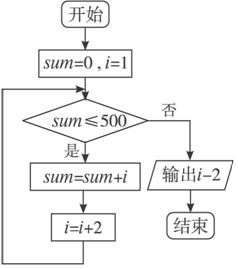
程序如下:
i=1;
sum=0;
while sum<=500
sum=sum+i;
i=i+2;
wend
print“最小自然数n的值为:”;i=i-2
end
点评 本题主要考查了循环结构,以及利用循环语句来实现数值的累加(乘),同时考查了流程图的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=±4x | B. | y=±2x | C. | y=±$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,4] | C. | [0,4] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2013) | B. | (-2013,0) | C. | (-∞,-2017) | D. | (-2017,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | (-3,3) | C. | (-4,2) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com