练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，直线AD与△ABC的外接圆相切于点A，若∠B=60°，则∠CAD等于（ ）

    A.30° B.60° C.90° D.120°

     

    B

    【解析】

    试题分析：由于弦切角∠DAC所夹弧的圆周角正好是∠B，因此可直接利用弦切角定理求解．

    【解析】
    ∵DA与△ABC的外接圆相切于点A，

    由弦切角定理得：

    ∴∠CAD=∠B=60°．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷（解析版） 题型：

    在空间直角坐标系O﹣xyz中，z=1的所有点构成的图形是 ．点P（2，3，5）到平面xOy的距离为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    已知二阶矩阵M有特征值λ=3及对应的一个特征向量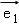=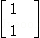，并且矩阵M对应的变换将点（﹣1，2）变换成（9，15）．求矩阵M．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：填空题

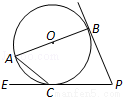
    （2014•汕头二模）如图，AB是圆O的直径，PB，PE分别切圆O于B，C，若∠ACE=40°，则∠P= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：填空题

    （2014•重庆）过圆外一点P作圆的切线PA（A为切点），再作割线PBC依次交圆于B、C，若PA=6，AC=8，BC=9，则AB= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

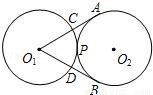
    如图，半径为2的两个等圆⊙O1与⊙O2外切于点P，过O1作⊙O2的两条切线，切点分别为A，B，与⊙O1分别交于C，D，则APB与CPD的弧长之和为（ ）

    A.2π B.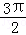 C.π D.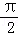

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    （2010•焦作二模）如图，已知PA为⊙O的切线，PBC为⊙O的割线，PA=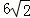，PB=BC，⊙O的半径OC=5，那么弦BC的弦心距OM=（ ）

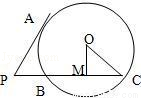
    A.4 B.3 C.5 D.6

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理（解析版） 题型：选择题

    圆内接四边形ABCD中，AD∥BC，AC与BD交于点E，在下图中全等三角形的对数为（ ）

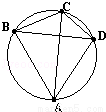
    A.2对 B.3对 C.4对 D.5对

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷（解析版） 题型：选择题

    已知复数z=1﹣i，则=（ ）

    A.2i B.﹣2i C.2 D.﹣2

     

    查看答案和解析>>

    同步练习册答案