
分析 (Ⅰ)由已知利用三角形面积公式可求a的值,进而利用余弦定理可求c的值.
(Ⅱ)由(Ⅰ)利用余弦定理可求cosB的值,结合范围B∈(0,π),利用同角三角函数基本关系式可求sinB,进而利用两角差的余弦函数公式计算求值得解.
解答 (本题满分为12分)
解:(Ⅰ)∵$C=\frac{π}{3},b=8$,△ABC的面积为$10\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{1}{2}×a×8$×sin$\frac{π}{3}$,解得:a=5,
∴由余弦定理可得:c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{25+64-2×5×8×\frac{1}{2}}$=7…6分
(Ⅱ)∵由(Ⅰ)可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{49+25-64}{70}$=$\frac{1}{7}$,
又∵B∈(0,π),可得:sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4\sqrt{3}}{7}$,
∴cos(B-C)=cosBcos$\frac{π}{3}$+sinBsin$\frac{π}{3}$=$\frac{4\sqrt{3}}{7}$×$\frac{\sqrt{3}}{2}$+$\frac{1}{7}×\frac{1}{2}$=$\frac{13}{14}$…12分
点评 本题主要考查了三角形面积公式,余弦定理,同角三角函数基本关系式,两角差的余弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
| 数据编号 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 道路里程数x | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
| 汽车保有量y | 144 | 154 | 160 | 168 | 176 | 180 | 186 | 190 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [1,3) | C. | [-3,∞) | D. | (-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | B. | $[kπ+\frac{5π}{12},kπ+\frac{11π}{12}](k∈Z)$ | ||
| C. | $[kπ-\frac{5π}{24},kπ+\frac{7π}{24}](k∈Z)$ | D. | $[kπ+\frac{7π}{24},kπ+\frac{19π}{24}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 32 | C. | 33 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
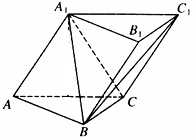 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,-1} | C. | {1,-1} | D. | {-1,0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com