
| A. | 1-a | B. | a-1 | C. | -1 | D. | 1 |
分析 令y=$\frac{lnx}{x}$,从而求导y′=$\frac{1-lnx}{{x}^{2}}$以确定函数的单调性及取值范围,再令$\frac{lnx}{x}$=t,从而化为t2+(a-1)t+1-a=0有两个不同的根,从而可得a<-3或a>1,讨论求解即可.
解答 解:令y=$\frac{lnx}{x}$,则y′=$\frac{1-lnx}{{x}^{2}}$,
故当x∈(0,e)时,y′>0,y=$\frac{lnx}{x}$是增函数,当x∈(e,+∞)时,y′>0,y=$\frac{lnx}{x}$是减函数;且$\underset{lim}{x→0}$$\frac{lnx}{x}$=-∞,$\frac{lne}{e}$=$\frac{1}{e}$,$\underset{lim}{x→+∞}$$\frac{lnx}{x}$=0;
令$\frac{lnx}{x}$=t,则可化为t2+(a-1)t+1-a=0,故结合题意可知,t2+(a-1)t+1-a=0有两个不同的根,
故△=(a-1)2-4(1-a)>0,故a<-3或a>1,不妨设方程的两个根分别为t1,t2,
①若a<-3,t1+t2=1-a>4,
与t1≤$\frac{1}{e}$且t2≤$\frac{1}{e}$相矛盾,故不成立;
②若a>1,则方程的两个根t1,t2一正一负;
不妨设t1<0<t2,结合y=$\frac{lnx}{x}$的性质可得,$\frac{ln{x}_{1}}{{x}_{1}}$=t1,$\frac{ln{x}_{2}}{{x}_{2}}$=t2,$\frac{ln{x}_{3}}{{x}_{3}}$=t2,
故(1-$\frac{ln{x}_{1}}{{x}_{1}}$)2(1-$\frac{ln{x}_{2}}{{x}_{2}}$)(1-$\frac{ln{x}_{3}}{{x}_{3}}$)
=(1-t1)2(1-t2)(1-t2)
=(1-(t1+t2)+t1t2)2
又∵t1t2=1-a,t1+t2=1-a,
∴(1-$\frac{ln{x}_{1}}{{x}_{1}}$)2(1-$\frac{ln{x}_{2}}{{x}_{2}}$)(1-$\frac{ln{x}_{3}}{{x}_{3}}$)=1;
故选D.
点评 本题考查了导数的综合应用及转化思想的应用,同时考查了分类讨论思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
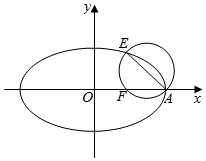 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆C过点$E(2e,\frac{b}{2})$,以AE为直径的圆恰好经过椭圆的右焦点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(1,+∞) | B. | (1,+∞) | C. | (-∞,1) | D. | (-1,1 ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 (B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )
(B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )| A. | PB⊥AD | B. | 平面PAB⊥平面PBC | ||
| C. | 直线BC∥平面PAE | D. | △PFB为等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}_{1}-{x}_{2}}{k}$ | B. | $\frac{{x}_{2}-{x}_{1}}{k}$ | C. | $\frac{|{x}_{1}-{x}_{2}|}{k}$ | D. | ±$\frac{{x}_{1}-{x}_{2}}{k}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com